Chapter 2 Mathematical foundation of cell-type deconvolution of biological data

In the previous chapter, I presented state-of-art of the current immuno-oncology research that has to embrace the vast complexity of cancer disease and the immune system. One part of this complexity can be explained by the presence and quantities of tumor-infiltrating immune cells, their interactions with each other and the tumor.

In this chapter, I will discuss how mathematical models can be used to extract information about different cell-types from ‘bulk’ omics data or how to de-mix mixed sources composing the bulk samples. To start with, I will introduce you to basic concepts of machine learning. Then I will focus on approaches adapted for cell-type deconvolution. In a literature overview, I will depict the evolution of the field as well as discuss the particularities of different tools for estimating presence and proportion of immune cells within cancer bulk omic data.

2.1 Introduction to supervised and unsupervised learning

Machine learning (ML) is a field of computer science where a system can learn and improve given an objective function and the data.

Mitchell gave a popular definition of machine learning in 1997:

Machine learning: A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P if its performance at tasks in T, as measured by P, improves with experience E.

— Mitchell in 1997 (Mitchell 1997)

Term Artificial intelligence (AI) is often used by the media or the general public to describe machine learning. Indeed ML can be considered as a branch of AI, together with computer vision and deep neural networks applications. However, commonly ML and AI are used interchangeably by the broad public.

ML is applied commonly in many fields of science and industry. I will not discuss here subtle differences between machine learning, statistical learning, computational statistics and mathematical optimization.

In general, algorithms can be divided into groups given the application:

• classification - aims to assign observations to a group (discrete variable)
• regression - aims to predict a continuous response of an input (continuous variable)
• clustering - aims to divide data into groups that are related to each other based on a distance

Another critical distinction can be made given the inputs to the algorithm. Here, I present the differences between supervised and unsupervised learning.

2.1.1 Supervised learning

Supervised learning can be described as “the analysis of data via a focused structure” (Piegorsch, n.d.). The primary task is to predict an output given the inputs. In the statistical language, the inputs are often called the predictors or the independent variables. In the pattern recognition literature, the term features are preferred. The outputs are called the responses, or the dependent variables. (Hastie, Tibshirani, and Friedman 2009)

The initial data is divided into two sets: training and test. First, the model is trained with correct answers on the training data (learning to minimize the error), and then its performance is evaluated on the test data.

Among widely used classifiers there are Support Vector Machines (SVM), partition trees (and their extension random forests), and neural networks. For regression, it is common to encounter linear regression, boosted trees regression,

2.1.2 Unsupervised learning

In Unsupervised learning is given the data and is asked to segment the data given a particular constraint. However, the true segments of the data are not known. Therefore an unsupervised algorithm aims to unveil the “hidden structure” of the data or latent variables.

One group of unsupervised learning are descriptive statistic methods, such as principal components, multidimensional scaling, self-organizing maps, and principal curves. These methods aim to represent to the data most adequately in low-dimensional space (Hastie, Tibshirani, and Friedman 2009).

Another group is clustering algorithms. Clustering is the way to create groups (multiple convex regions) based on the intrinsic architecture of the data. These groups are not necessarily known beforehand but can be validated with the domain knowledge. Popular clustering algorithms are k-means, hierarchical clustering, mixture density-based clustering (Xu and Wunsch 2008).

In both descriptive statistics and clustering, one important parameter (i.e. denoted \(k\)) is the number (number of factors, variables, clusters) to which the data should be decomposed. Different algorithms and applications can propose an automatic choice of \(k\) based on formal indexes or previous knowledge, in others, the user needs to provide the \(k\).

2.1.3 Low-dimensional embedding for visualization

There is a common confusion, often seen in computational biology, between dimension reduction and clustering. This confusion is highly pronounced with, a popular in biology, algorithm: T-distributed Stochastic Neighbor Embedding (t-SNE) (Van Der Maaten and Hinton 2008). t-SNE works in 2 main steps: (1) a probability distribution over pairs of high-dimensional objects is computed in such a way that similar objects have a high probability of being picked, whilst dissimilar points have an extremely small probability of being picked, (2) t-SNE defines a similar probability distribution over the points in the low-dimensional map, and it minimizes the Kullback–Leibler divergence between the two distributions with respect to the locations of the points in the map. It is not reliable to use t-SNE for clustering as it does not preserve distances. It can also easily overfit the data and uncover ‘fake’ or ‘forced’ patterns. Therefore, a clustering should not be applied to t-sne reduced data. An alternative to the t-SNE method is recently published Uniform Manifold Approximation and Projection for Dimension Reduction (UMAP) (Mcinnes and Healy 2018)– that is based on Laplacian eigenmaps, highly scalable, reproducible and recently applied to biological data (Becht et al. 2018). Older used alternatives are ISOMAPS (non-linear dimension reduction) or PCA (Principal components analysis). For any non-linear dimension reduction method, it is not recommended to use clustering a posteriori. Clusters should be computed on original data, and then the cluster labels can be visualized in low-dimensional embedding.

2.2 Types of deconvolution

One specific application of mathematical/statistical tools is deconvolution of mixed signals.

According to a mathematical definition:

Deconvolution : the resolution of a convolution function into the functions from which it was formed in order to separate their effects. (“deconvolution | Definition of deconvolution in English by Oxford Dictionaries” 2018)

Alternatively, in plain English:

a process of resolving something into its constituent elements or removing complication (“deconvolution | Definition of deconvolution in English by Oxford Dictionaries” 2018)

The similar problem of mixed sources can be encountered in other fields, i.e., signal processing, also known under the name of “cocktail party problem.” In the cocktail party problem, at a party with many people and music, sound in recorded with several microphones. Through blind source separation, it is possible to separate the voices of different people and the musical background (Fig. 2.1) (Cherry 1953).

Figure 2.1: Illustration of the cocktail party problem. During a cocktail party voices of participants can be recorded with a set of microphones and then recovered through blind source separation. The illustration purposes only four sources are mixed with three microphones, in reality, the analysis can be performed with many sources. However, a number of samples (microphones) should be higher than the number of sources (contrary to the illustration).

The same concept can be transposed to the bulk omic data, each biological species (like gene) is a cocktail party where each sample is a microphone that gathers mixed signals of different nature. The signals that form the mixtures can be different depending on the data type, and the scientific question asked.

In general, the total bulk data can be affected by three abundance components (Shen-Orr and Gaujoux 2013):

1. sample characteristic (disease, clinical features)
2. individual variation, genotype-specific or technical variation
3. presence and abundance of different cell types expressing a set of characteristic genes

Many scientists invested their efforts in order to dissect the bulk omic data into interpretable biological components.

In scientific literature, there can be encountered three main understanding of tumor deconvolution:

• estimating clonality: using genomic data is it possible to trace tumor phylogeny raised from mutations and aberrations in tumor cells; therefore it is dissecting intra-tumor heterogeneity (i.e., using transcriptomic data (Schwartz and Shackney 2010), or more often CNA data (see Section 2.4.2)
• estimating purity: deconvolution into the tumor and immune/stroma compartments, often aiming to “remove” not-tumor signal from the expression data, can be performed with different data types, the most reliable estimations are usually obtained from CNA data (see Section 2.4)
• estimating cell-type proportions and/or profiles from bulk omics data, most of works were performed on transcriptome data (see Section 2.3) and some on the methylome data (see Section 2.4.1)

These three types of deconvolution can be performed on the bulk omics data. Here we will focus on cell-type deconvolution models using bulk transcriptome. I will also briefly introduce deconvolution models applied to other data types (methylome and CNA).

2.3 Cell-type deconvolution of bulk transcriptomes

The idea of un-mixing the bulk omic profiles is documented to first appear in an article of Venet et al. (2001) as a way to

infer the gene expression profile of the various cell types (…) directly from the measurements taken on the whole sample

In the primary hypothesis (Abbas et al. 2009), a mixture of signals from TME in transcriptomic samples can be described as a linear mixture.

\[ X = SA \tag{2.1} \]

Where in Equation (2.1) \(X\) is microarray data matrix of one biological sample, \(A\) are mixing proportions, and \(S\) is the matrix of expression of genes in each cell type.

Algebraically the same problem can be formalized as the latent variable model:

\[ \forall i \in \{1,M\}, \forall j \in \{1,N\} \\ x_{ij}= \sum_{k=1}^K a_{kj} *s_{ik}+ e_{ij} \tag{2.2} \]

Where \(x_{ij}\) is expression of gene \(i\) in sample \(j\), \(a_{kj}\) is the proportion of cell type \(k\) in sample \(j\) and \(s_{ik}\) is the expression of the gene \(i\) in the cell type \(k\), \(K\) total number of cell types, \(N\) total number of samples, \(M\) total number of genes. The error term \(e_{ij}\) cannot be directly measured.

The goal of deconvolution is to reverse these equations and starting from the mixture infer the \(A\) (or \(a_{kj}\)) and \(S\) (or \(s_{ik}\)).

Graphically the deconvolution of bulk gene expression can be depicted as in Fig. 2.2.

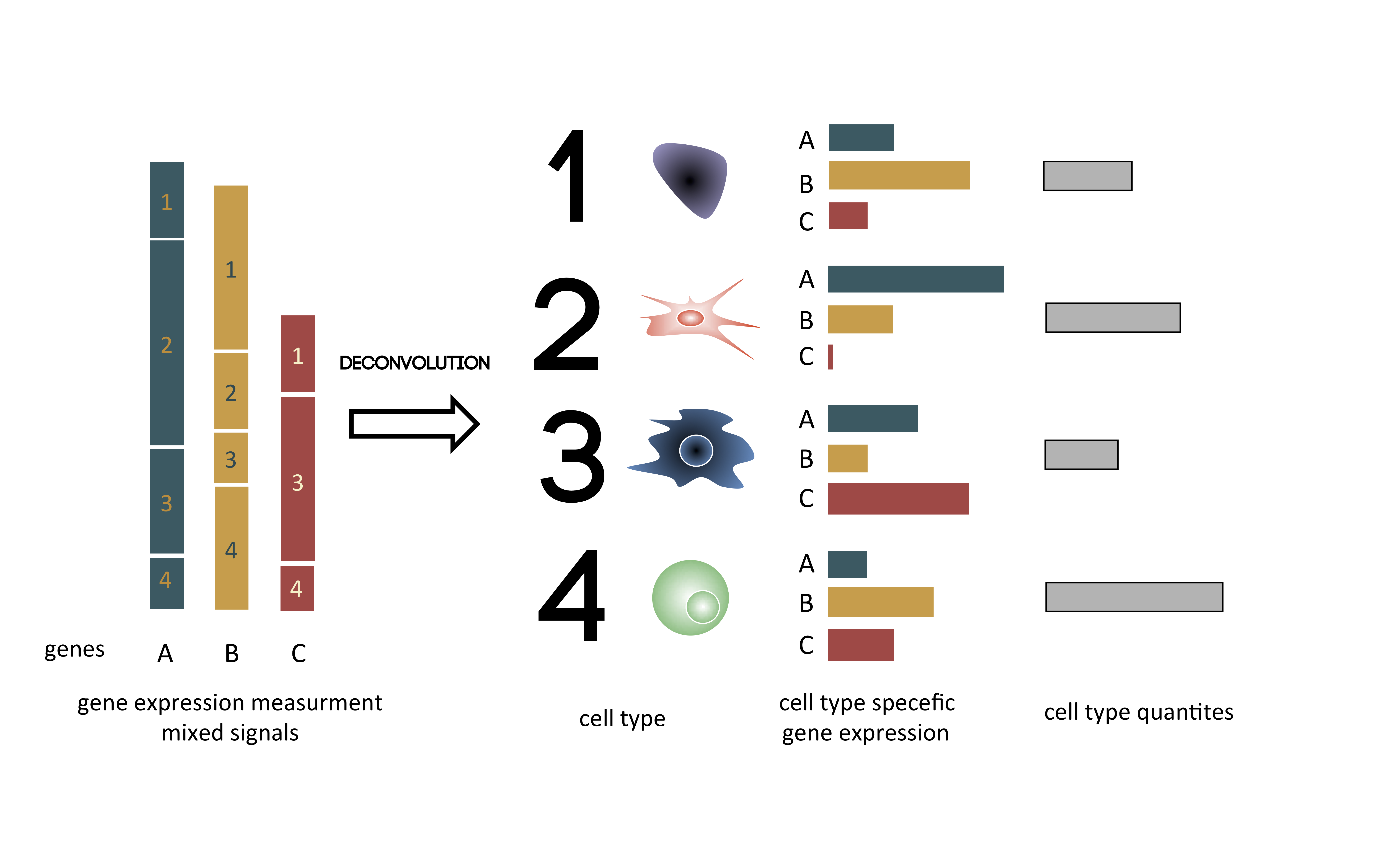
Figure 2.2: Principle of the deconvolution applied to transcriptome Graphical illustration of the deconvolution of mixed samples. Starting from the left, gene expression of genes A B C is a sum of expression of cell types 1, 2, 3, 4. After deconvolution, cell types are separated, and gene expression of each cell type is estimated taking into account cell type proportions.

However, in this model, either the mixing proportions, number of mixing sources or an array of specific genes need to be known. While, in the real-life case, only \(X\) is truly known. Therefore, developed models proposed various manners for estimating the number of mixing sources and their proportions, or the specific cell type expression.

Why there is a need for cell-type deconvolution approaches?

• for differential gene expression analysis, to avoid confusion between a studied condition (i.e. disease impact) and cell-type abundance (change in gene expression due to the change of cell proportions)
• difference in gene expression in one cell type can be blurred by the presence of other cells expressing the gene
• to obtain information about a fraction of given component in the sample
• to study potential interactions between cell types in the studied context
• to infer context-specific profile or signature

2.3.1 Literature overview

In order to answer general and specific need for cell-type deconvolution of bulk transcriptomes researches produced a large collection of tools. I have collected all (to my knowledge) articles published in journals or as a pre-print (up to May 2018) that propose original models/tools of cell-type deconvolution of bulk transcriptomes (Tab. 2.1). Therefore clonal deconvolution methods are not included in this overview. The transcriptome-based purity estimation methods are included as many of them proposed an initial 2-sources model that could be, at least in theory, extended to multiple sources model. Also, I did not include cell-type deconvolution methods of other data types (such as methylome). A separate section 2.4 is dedicated to non-transcriptome methods.

####Growth of the field

The Table 2.1 contains 64 (including mine) deconvolution methods. It can be observed (Fig. 2.3) that since the begging of my thesis (2015) the number of publications has doubled (64 publications in 2018 vs. 33 in 2014). Also, from 2014 on, more methods are published every year. In Fig. 2.3 hallmark publications are indicated in red above their year of publication. The three most popular methods (based on number of citations/number of years since publication) are CIBERSORT (Newman et al. 2015) (2015, total number of citations: 343 and 88.75 citations per year), ESTIMATE (Yoshihara et al. 2013) (2013, total number of citations: 266 and 44.33 citations per year), and csSAM (Shen-Orr et al. 2010) (2010, total number of citations: 286 and 31.77 citations per year). It can be noticed that the high impact of the journal plays a role, the top 3 cited methods were published in Nature Methods and Nature Communications followed by Virtual Microdissection method (Moffitt et al. 2015) (2015) published in Nature Genetics. However, the fifth most cited publication Abbas et al. (2009) (2009, a total of 207 citations) appeared in PLOS ONE. As the index is a bit penalizing for recent publications, among commonly cited tools after 2015 are MCPcounter with 42 citations (2016, 32 without self-citations) and xCell with 14 citations (2017, 11 without self-citations). A big number of publications with a low number of citations were published in Oxford Bioinformatics or BMC Bioinformatics which underlines the importance of publishing a computational tool along with an important biological message rather than in a technical journal in order to increase a chance to be used by other researchers.

2.3.1.1 Availability

Another essential aspect is the availability of the tool. One-third (in total 21) methods do not provide source code or a user-interface tool to reproduce their results. Among those articles, 13 was published before 2015. Therefore, it can be concluded that the pressure of publishers and research community on reproducibility and accessibility of bioinformatic tools gives positive results. Shen-Orr and Gaujoux (2013), authors of semi-supervised NMF method (Gaujoux and Seoighe 2012), published CellMIx: a comprehensive toolbox for gene expression deconvolution where he implements most of previously published tools in R language and group them in the same R-package. This work tremendously increased the usability of previously published deconvolution methods. The CellMix package is one of the state-of-the-art work on deconvolution that regroups algorithms, signatures and benchmark datasets up to 2013.

Table 2.1: Summary of methods for cell-type deconvolution of bulk transcriptome

The most popular language of implementation of published methods is R (49.2 %), followed by Matlab (11.11%), only one tool so far was published in Python.

2.3.1.2 Data type

Also, most of the methods were designed to work with microarray data. There is a high chance that some of them are adaptable to RNA-seq. However, a little number of older methods was tested in a different setup. For some method, as CIBERSORT, demonstrated to work with microarray and applied commonly to RNA-seq by other researchers, the validity of results remains unclear as some studies claim that CIBERSORT performs accurately applied to RNA-seq (Thorsson et al. 2018) and other opt against it (Li, Liu, and Liu 2017; Tamborero et al. 2018). Most of newer methods (i.e. EPIC (Racle et al. 2017), quanTIseq (Finotello et al. 2017) or Infino (Zaslavsky et al. 2017)) are specifically designed for RNA-seq TPM-normalized data. Some methods, mostly enrichment-based methods, are applicable to both technologies (i.e. xCell (Aran, Hu, and Butte 2017)).

2.3.1.3 Objectives of the cell-type deconvolution

It is remarkable that the general aim of the cell-type deconvolution changed with time. The earlier methods aimed to improve the power of differential expression analysis though purification of the gene expression. For example, to compare differentially expressed genes (DEG) in T-cell from the blood under two conditions. However, the obtained purified profiles from complex mixtures were often uncertain (Onuchic et al. 2016). Recently, the most mentioned goal of deconvolution is a quantification of proportions of different cell types, especially in the context of cancer transcriptomes motivated by redefinition of immunophenotypes discussed in the previous chapter. The most popular tissue of interest for deconvolution algorithms are cancer tissues and blood. Other applications are cell-cycle time-dependent fluctuations of yeast, brain cells, and glands .

2.3.1.4 Differences between approaches

Mathematically speaking, I have divided methods into four categories: probabilistic, regression, matrix factorisation and convex hull depending on the nature of the approach. Most of the methods (48 - 74.6%) are working within a supervised framework, and only 20% (14) are unsupervised. The approaches will be described in detail in the following section.

There are numerous practical differences between the methods. Shen-Orr and Gaujoux (2013) in their review of deconvolution tools grouped the tools depending on their inputs and outputs. Given the type of outputs, deconvolution can be considered as complete (proportions and cell profiles) or partial (one of those). Moreover, the inputs of the algorithms can be important to evaluate how practical the tool is. The most popular tools and the most recent tools ask for minimal input from the user: the bulk gene expression matrix, or even raw sequencing data (Finotello et al. 2017). Older methods usually request either at least approximative proportions of mixed cells or purified profiles to be provided. The newer methods include the reference profiles in the tool if necessary. Some tools, including most of purity estimation tools, demand an additional data input as normal samples or another data type such as CNA data (Timer (Li and Xie 2013), VoCAL (Steuerman and Gat-Viks 2016)) or image data (quanTIseq (Finotello et al. 2017)). An important parameter is also a number of sources (\(k\)) to which the algorithm deconvolutes the mixture. In many methods, it should be provided by the user, which can be difficult in a case of complex mixtures of human tissues. Besides, type of method can also limit the number of sources, for example, a probabilistic framework privilege lower number of sources (2-3) due to the theoretical constraints. In regression depending on provided reference the output number of estimated sources is imposed. Because of the problem of collinearity and similarity of immune cell profiles, it is hard to distinguish between cell sub-types, deconvolution into fine-grain cell subtypes is often called often deep deconvolution. Some methods (i.e., CIBERSORT, Infino, xCell) give specific attention to deconvolution of cell-subtypes. An absolute presence of a cell type in the mixture can also be an essential factor. If it is too low it can reach a detection limit, Electronic subtraction (Gosink, Petrie, and Tsinoremas 2007) discuss specifically the detection of rare cel-types.

2.3.1.5 Computational efficiency

Running time and the necessary infrastructure are another way to characterize the methods. Although it is hard to compare the running time objectively simultaneously of all the tools because of the heterogeneity of methods and different datasets analysed, some tendencies can be observed. If one thinks about applying deconvolution methods to big cohorts, regression and enrichment-based methods should be well suited. As far as matrix factorisation is concerned, it depends on the implementation (i.e. R vs Matlab) and if the number of sources needs to be estimated (multiple runs for different \(k\) parameter) or if a stabilisation needs to applied (multiple runs for the same \(k\) parameter). Finally, probabilistic tools seem to be challenging to scale, i.e. authors of Infino admit that their pipeline is not yet applicable at high-throughput.

In order to let user better understand the differences between different mathematical approaches, I will introduce shortly the types of approaches used for cell-type deconvolution of transcriptomes as well as their strong and weak points.

Figure 2.3: Distribution of publications of cell-type deconvolution of bulk transcriptome over the years. In red: hallmark publications. Data gathered based on PubMed and google scholar search in May 2018.

Figure 2.4: Simple statistics illustrating characteristics of published cell-type deconvolution tools: a) Percentage of used approach type, b) Percentage of supervised/ unsupervised tools, c) Percentage of the programming languages of implementation. Data gathered based on pubmed and google scholar search in May 2018.

2.3.2 Regression-based methods

Regression models are the most popular methods for bulk gene expression deconvolution. They use estimated pure cell profiles as depending variables (or selected signature genes) that should explain the mixed profiles choosing best \(\beta\) parameters (Eq. (2.3)) that can be interpreted as cell proportions.

A standard type of regression is called linear regression. It reflects linear dependence between independent and dependent variables. The linear regression was developed in the precomputer age of statistics (Hastie, Tibshirani, and Friedman 2009).

In linear regression, we want to predict a real-valued output \(Y\), given a vector \(X^T = (X_1,X_2,… ,X_p)\). The linear regression model has the form:

\[\begin{equation} f(X) = \beta_0 + \sum_{j=1}^{p} X_j\beta_j \tag{2.3} \end{equation}\]

Where the \(\beta_j\)s are unknown parameters or coefficients, and \(X_j\)s are the explaining variables. Given pairs of (\(x_1\),\(y_1\))…(\(x_N\) ,\(y_N\) ), one can estimate coefficients \(\beta\) with an optimization of an objective function (also called cost function).

The most popular estimation method is least squares, the coefficients \(\beta = (\beta_0, \beta_1, ..., \beta_n)\) are computed to minimize the residual sum of squares (RSS):

\[\begin{equation} RSS(\beta) = \sum_{i = 1}^{N}(y_i - f(x_i))^2 = \sum_{i = 1}^{N}(y_i - \beta_0 - \sum_{j=1}^p x_i\beta_j)^2 \tag{2.4} \end{equation}\]

Ordinary least squares regression is using Eq.(2.4) to compute \(\beta\).

Ridge regression (Eq.(2.5)) (aka Tikhonov regularization) adds a regularizer (called \(L2\) norm) to shrink the coefficients (\(\lambda \geq 1\)) through imposing a penalty on their size.

\[\begin{equation} \hat{\beta}^{ridge} = \underset{\beta}{\text{argmin}}\{\sum_{i = 1}^{N}(y_i - f(x_i))^2 + \lambda\sum_{j=1}^{p}\beta^2_j\}\tag{2.5} \end{equation}\]

Similarly Lasso regression (Equation (2.6)) adds a regularization term to RSS (called \(L1\) norm), it may set coefficients to 0 and therefore perform feature selection.

\[\begin{equation} \hat{\beta}^{ridge} = \underset{\beta}{\text{argmin}}\{\sum_{i = 1}^{N}(y_i - f(x_i))^2 + \lambda\sum_{j=1}^{p}\lvert\beta_j\rvert\}\tag{2.6} \end{equation}\]

In Elastic net regression both penalties are applied.

Support Vector Regression (SVR) is regression using Supported Vector Machines (SVM). In SVR \(\beta\) can be estimated as follows:

\[\begin{equation} H(\beta,\beta_0) = \sum_{i=1}^{N} V (y_i − f(x_i)) +\frac{λ}2\lVert\beta\rVert^2 \tag{2.7} \end{equation}\]

where error is measured as follows:

\[\begin{equation} V_\epsilon(r) = \begin{cases} 0, & \text{if $\lvert r \rvert < \epsilon$,}\\ \rvert r\lvert - \epsilon, & \text{otherwise}. \end{cases} \tag{2.8} \end{equation}\]

with \(\epsilon\) being the limit of error measure, meaning errors of size less than \(\epsilon\) are ignored.

In the SVM vocabulary, a subset of the input data that determine hyperplane boundaries are called the support vectors (Fig.2.5). SVR discovers a hyperplane that fits the maximal possible number of points within a constant distance, \(\epsilon\), thus performing a regression.

In brief, in SVR, RSS is replaced by a linear \(\epsilon\)-insensitive loss function and uses L2-norm penalty function. There exist variants of SVR algorithm, i.e. \(\epsilon\)-SVR (Drucker et al. 1997) and \(\nu\)-SVR (Schölkopf et al. 2000). \(\epsilon\)-SVR allows to control the error; this favors more complex models. In the \(\nu\)-SVR the distance of the \(\epsilon\) margin can be controlled and therefore the number of data points used for regression can be controlled. Ju et al. (2013) used an SVM-based method to define cell type-specific genes. A model using \(\nu\)-SVR with linear kernel was used by Newman et al. (2015) in CIBERSORT.

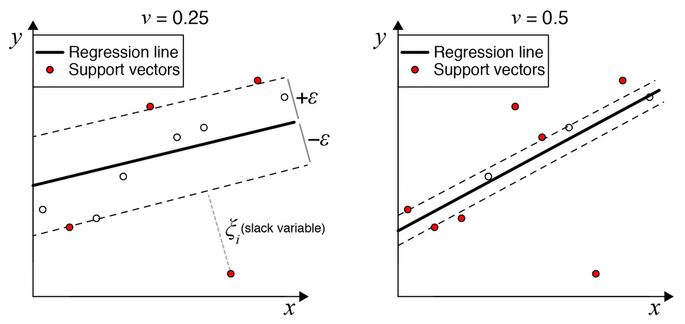
Figure 2.5: Principle of the SVR regression. In SVR regression \(\epsilon\) represents the limit of error measure, input data points higher than \(+\epsilon\) or lower than \(-\epsilon\) are called support vectors. The \(\nu\) parameter in \(\nu\)-SVR regression controls the distance of training error bonds: left - lower \(\nu\) value larger bound, right - higher \(v\) margin, smaller bound. Reprinted by permission from Springer Nature (Newman et al. 2015) © 2018 Macmillan Publishers Limited, part of Springer Nature. All rights reserved.

As unconstrained optimization of the objective function can result in negative coefficients, in the context of cell-type deconvolution, authors often aim to avoid as it complicates the interpretation. Therefore, different constraints can be imposed on the \(\beta\) coefficients. The most common conditions are \(\beta_0 +\beta_1+ ...+\beta_n =1\) and \(\forall\beta_i \geq 0\). Solution respecting the non-negativity condition is also called non-negative least squares (NNLS) to contrast with ordinary least squares (OLS). NNLS was adopted by many authors (Venet et al. 2001; Abbas et al. 2009; Repsilber et al. 2010; Zuckerman et al. 2013; Wang et al. 2016).

The task can also be solved differently from the computational perspective. Lu, Nakorchevskiy, and Marcotte (2003) and Wang, Master, and Chodosh (2006) propose to use simulated annealing to minimize the cost function. Gong et al. (2011) proposed to solve the task using quadratic programming.

An extensive review on optimization of the objective function for regression methods in cell-type deconvolution was published by Mohammadi et al. (2017). Authors carefully consider different possibilities of parameter choice in the loss and regularization formulations and its performance. They present as well recommendations for construction of basis matrix and data pre- and post-processing. Digital tissue deconvolution (DTD) (Görtler et al. 2018) aims to train the loss function with in silico mixtures of single cell profiles resulting in improved performance of rare cell types (present in a small proportion). However, the training is computationally heavy, and the proper training data for bulk transcriptomes are not available.

Since the publication of CIBERSORT (Newman et al. 2015) some authors (Chen et al. 2018; Schelker et al. 2017) used the Newman et al. (2015) implementation directly with pre/post modifications or with different basis matrix or they re-implemented the SVR regression in their tools (Chen et al. 2018).

Another recent method EPIC (Racle et al. 2017) introduced weights related to gene variability. In their constrained regression, they add it explicitly in the cost function modifying RSS (Eq.(2.4)):

\[\begin{equation} RSS^{weighted} (\beta) = \sum_{i = 1}^{N}(y_i - \beta_0 - w_i \sum_{j=1}^p x_i\beta_j)^2 \tag{2.9} \end{equation}\]

with the non-negativity and the sum constraints, we discussed above. The \(w_i\) weights are corresponding to the variance of the given gene measure in the same cell type. It aims to give less importance to the genes variant between different measurements of the same cell-type. EPIC also allows a cell type that is not a referenced in the signature matrix with an assumption that the non-referenced cell type is equal to 1- a sum of proportions of other cell types (Eq.(2.10)). Authors interpret this non-referenced cell type as the tumor fraction:

\[\begin{equation} \beta_m = 1 - \sum_{j=1}^{m-1}\beta_j \tag{2.10} \end{equation}\]

An additional feature of EPIC is advanced data normalization and estimation of mRNA produced by each cell to adjust cell proportions, which was previously proposed by Liebner, Huang, and Parvin (2014) in the context of microarray data:

\[\begin{equation} p_j=\alpha \frac{\beta_j}{r_j} \tag{2.11} \end{equation}\]

where \(p_j\) are actual cell proportions that are ‘normalized’ with empirically derived coefficient \(\alpha\) and measured \(r_j\) is the number of RNA nucleotides in cell type \(j\).

Recently CIBERSORT proposed an absolute mode where the proportions are not relative to the leucocyte infiltration but to the sample. It can be obtained with an assumption that the estimation of the proportion of all genes in CIBERSORT matrix is corresponding to sample purity. This functionality was not yet officially published, and it is still in experimental phase (Newman, Liu, and Alizadeh 2018).

Regression methods combined with pre- and post-processing of data can result in estimation of proportions that can be interpreted directly as a percentage of cells in a mixed sample. It is an important feature hard to achieve with other methods. Some methods provide relative proportions of the immune infiltrate (Newman et al. 2015) and another aim to provide absolute abundance (Racle et al. 2017). The absolute proportions are easily comparable between data sets and cell types. Regression-based methods are usually quite fast and can process large transcriptomic cohorts. However, as I will discuss in Validation section, they pose on the hypothesis that the reference profiles available in some context (i.e., blood) are valid in a different one (i.e., tumor) or that profiles extracted from one data type (scRNA-seq) are adapted to deconvolute bulk RNAseq. Most of the recent regression methods focused on estimating proportions and do not estimate context-specific profiles and can process as little as one sample.

2.3.3 Enrichment-based methods

Table 2.2: Contingency table is the count of overlap of genes present in a certain condition (Y) vs. not present (Y-Z) and association to a pathway X (in X or not in X). The contingency table is used in the frequency based test as Fisher exact test.

	Y	Z-Y
in X	a	b
not in X	c	d

Enrichment-based methods aim to evaluate an amount of activity of a given list of genes within the data. This can be obtained by calculating a score based on gene expression. Traditionally enrichment methods were used to analyze set of DEG. Different statistical approaches were adapted: like Fisher exact test giving a p-value that estimated the chance a given list of genes is over/under present in the input list of DEGs and therefore characterize the condition vs. control expressed genes.

Let’s take an example; if one wants to compute enrichment in pathway X of the list of DEG genes Y with the total number of tested genes Z, a contingency table need to be constructed (Tab. 2.2).

In the Fisher exact test formula (Eq. (2.12)) the \(a\), \(b\),\(c\) and \(d\) are the individual frequencies, i.e. number of genes in of the 2X2 contingency table, and \(N\) is the total frequency (\(a + b + c + d\)).

\[\begin{equation} p= \frac{( ( a + b ) ! ( c + d ) ! ( a + c ) ! ( b + d ) ! )}{a ! b ! c ! d ! N ! } \tag{2.12} \end{equation}\]

Another important (>14000 citations) algorithm computing such a score (enrichment score ES) is named gene set enrichment analysis (GSEA) (Subramanian et al. 2005) uses sum-statistics. The list of genes user wants to test for enrichment is usually ranked by fold change odd or p-value of DGE analysis.

The high score indicated high activity of genes included in the list. GSEA can also indicate an anti-activity of correlation. A variant of GSEA, single sample GSEA (ssGSEA) (Barbie et al. 2009) was used by Şenbabaoğlu et al. (2016), Yoshihara et al. (2013) and Aran, Hu, and Butte (2017) to compute infiltration scores. In the ssGSEA genes are ranked by their absolute expression. A variance-based variant of GSEA - GSVA (Hänzelmann, Castelo, and Guinney 2013) was used by Tamborero et al. (2018) for the same purpose. MCPcounter (Becht et al. 2016) uses an arithmetic mean of gene expression of highly specific signature genes to compute a score.

In this way obtained scores, are not comparable between different cell types and datasets. Therefore some authors propose normalization procedures that make the score more comparable. For instance, xCell uses a platform-specific transformation of enrichment scores. Similarly, Estimate transforms scores for TCGA though an empirically derived formula. MCPcounter authors use z-scoring to minimize platform-related differences. Unfortunately, the normalization is not directly included in the R package

Even though enrichment methods do not try to fit the linear model and derived scores are not mathematically conditioned to represent cell proportions; usually there can be observed a strong linear dependence. An advantage of the enrichment-based methods is the speed and possibility to include distinct signatures that can characterize cell-types and cell-states of different pathways.

2.3.4 Probabilistic methods

The probabilistic methods share a common denominator: they aim to minimise a likelihood function of Bayes’ theorem:

\[\begin{equation} p(y|\theta) = \frac{p(\theta|y )* p(y)}{p(\theta)} \tag{2.13} \end{equation}\]

In Eq.(2.13) \(y\) is our data, \(\theta\) a parameter, \(p(y|\theta)\) posterior, \(p(\theta|y )\) likelihood and \(p(\theta)\) prior. Prior distribution is what we know about the data before it was generated and combined with a probability distribution of the observed data is called posterior distribution. The likelihood describes how likely it is to observe the data (\(y\)) given the parameter \(\theta\) (probability of \(y\) given \(\theta\) - \(p(y|\theta)\)). A parameter is characteristic of a chosen model and a hyperparameter is a parameter of prior distribution.

In the literature, there are mainly different types of probabilistic models, one that assumes some type of distribution of mixed sources (i.e., Gaussian or Poisson), others that learn the distribution parameters empirically from a training set, another that try to find the parameters of the distribution given the number of given sources. Then in each case, there are different ways of constructing different priors and posteriors functions. Among used techniques are Markov Chain Monte Carlo or Expectation-Maximisation, which themselves can be implemented in different ways (Erkkilä et al. 2010; Ghosh 2004; Lähdesmäki et al. 2005; Li and Xie 2013; Roy et al. 2006, Zaslavsky et al. (2017)).

The probabilistic approaches are the most popular for purity estimation (2 components models), that seems to be possible to extend to 3-components model (Wang et al. 2017). As far as cell-type decomposition into a number of cells is concerned, a method published on BioRxiv Infino uses Bayesian inference with a generative model, trained on cell type pure profiles. Authors claim their method is notably suited for deep deconvolution that is able to build cell type similarities and estimate the confidence of the estimated proportions which help to interpret the results better.

A probabilistic framework is an attractive approach with solid statistical bases. It can be suited to many specific cases. The pitfalls are (1) the need of prior profiles or correct hypothesis on the distribution parameters (2) reduced performance when applied to high dimensional datasets due to extensive parameters search.

2.3.5 Convex-hull based methods

An emerging family of BSS methods is convex geometry (CG)-based methods. Here, the sources are found by searching the facets of the convex hull spanned by the mapped observations solving a classical convex optimization problem (Yang et al. 2015). It can be implemented in many ways (Preparata and Shamos 1985).

Convex hull can be defined as follows (Erickson, Jeff 2018):

We are given a set \(P\) of \(n\) points in the plane. We want to compute something called the convex hull of \(P\). Intuitively, the convex hull is what you get by driving a nail into the plane at each point and then wrapping a piece of string around the nails. More formally, the convex hull is the smallest convex polygon containing the points:

• polygon: A region of the plane bounded by a cycle of line segments, called edges, joined end-to-end in a cycle. Points, where two successive edges meet, are called vertices.

• convex: For any two points \(p\), \(q\) inside the polygon, the line segment \(pq\) is completely inside the polygon.

• smallest: Any convex proper subset of the convex hull excludes at least one point in \(P\). This implies that every vertex of the convex hull is a point in \(P\).

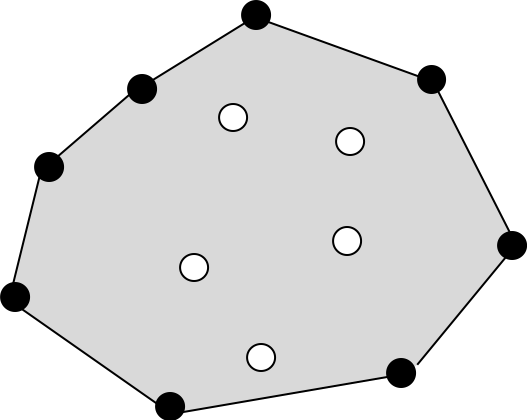
Figure 2.6: Convex hull illustration. A set of points and its convex hull (line). Convex hull vertices are black, and interior points are white. Image reproduced after Erickson, Jeff (2018).

Convex hull methods have been used in many fields, from economics and engineering, I will discuss it with a focus on biological context to link tightly to cell-type deconvolution.

The central assumptions of Convex hull optimization are that the gene expression of pure cell types is non-negative and that cell type proportions are linearly independent.

The shapes can be fitted to a cloud of points in many ways in order to respond to given optimality criteria. A popular method introduced by Shoval et al. (2012) and applied to gene expression and morphological phenotypes of biological species employ the Pareto front concept which aims to find a set of designs that are the best trade-offs between different requirements.

Visually Pareto front correspond to the edge of the convex hull.

Wang et al. (2013) proposed Complex Analysis of Mixtures (CAM) method to find the Pareto front (the vertices of \(X\) mixed matrix (a convex set)). In the context of the cell-type deconvolution, it can be said that “the scatter simplex of pure subpopulation expressions is compressed and rotated to form the scatter simplex of mixed expressions whose vertices coincide with cell proportions”(Wang et al. 2016). In respect to the assumptions, under a noise-free scenario, novel marker genes can be blindly identified by locating the vertices of the mixed expression scatter simplex (Fa-Yu Wang et al. 2010). In the figure (Fig. 2.7), the \(a_i\)’s are cell-type proportions of \(k\) cell types, \(s_i\) pure cell type expression and \(x_j\) mixed expression in sample \(j\). Therefore the vertices correspond to the column vectors of the matrix \(A\) (Eq. (2.1)). The genes placed in a distance \(d\) from the vertices can be interpreted as marker genes.

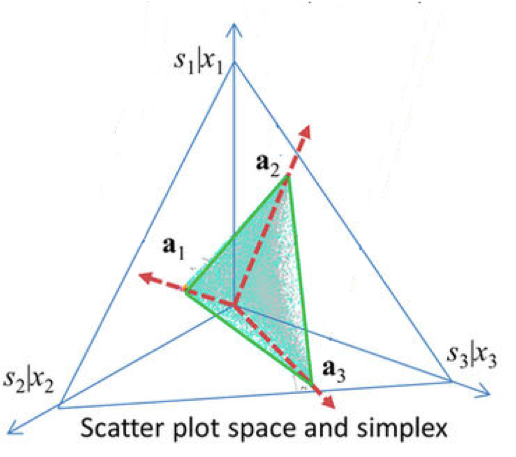
Figure 2.7: Fitting gene expression data of mixed populations to a convex hull shape. The geometry of the mixing operation in scatter space that produces a compressed and rotated scatter simplex whose vertices host subpopulation-specific marker genes and corresponding to mixing proportions.

In the procedure suggested by Wang et al. (2013), before performing CAM, clustering (more precisely affinity propagation clustering (APC) ) is applied to the matrix in order to select genes representing clusters, called cluster centers \(g_m\) and dimension reduction(PCA) is applied to the sample space. Then in order to fit a convex set, a margin-of-error should be minimized. The Eq. (2.14) explains the computation of the error which computes \(L2\) norm of the difference between \(g_m\) possible vertices and remaining exterior clusters. All possibilities of combinations drew from \(C^M_K\), \(M\) number of clusters and \(K\) true vertices, are tested.

\[ \text{given }\alpha_k \geq 0, \sum^K_{k=1}\alpha_k=1 \\ \delta_{m, \{1,...,K\} \in C^M_K }= \underset{\alpha_k}{min} \sqrt{{g_m} - \sum^K_{k=1}\alpha_kg_k} \tag{2.14} \]

Once optimal configuration is found, the proportions are computed using standardised averaging: \[\begin{equation} \hat{\alpha_k} = \frac{1}{n_{markers}} \sum_{i \in markers} \frac {x(i)}{\rVert x(i)\lVert} \end{equation}\] where \(\hat{\alpha_k}\) is proportion of cell type \(k\), \(n_{markers}\) number of marker genes (obtained from CAM), and \(\rVert x(i)\lVert\) is the \(L1\) or \(L2\) norm of a given marker gene \(x_i\).

Then the cell-type specific profiles are obtained with linear regression. Authors of CAM also propose a minimum description length (MDL) index that determines the number of sources in the mixture. It selects the \(K\) minimizing the total description code length.

So far, the published R-Java package CAM does not allow to extract gene specific signatures, and it is not scalable to large cohorts (many samples). In the article, authors apply essential pre-processing steps that are not trivial to reproduce and which are not included in their tool. Authors apply CAM and validate on rather simple mixtures (tissue in vitro mixtures and yeast cell cycle).

A slightly different approach was proposed by Newberg et al. (2018). It does not require initial dimension reduction steps or clustering before fitting the convex hull, and it is based on a probabilistic framework. The toll CellDistinguisher was inspired by topic modeling algorithm (Arora et al. 2013). It first computes \(Q\) matrix (Eq. (2.15)). Then each row vector of \(Q\) is normalized to 1 giving \(\overline{Q}\) matrix. Every row of \(\overline{Q}\) lies in the convex hull of the rows indexed by the cell-type specific genes. Then \(L_2\) norm of each row is computes. Genes which rows have the highest norm can be used as distinguishers or marker genes. Then other runs of selections are applied after recentering the matrix to find more markers.

\[\begin{equation} Q=XX^T \tag{2.15} \end{equation}\]

Once the set of possible distinguishers is defined, proportions and cell profiles are computed using a Bayesian framework to fit the convex hull. Authors provide a user-friendly R package CellDistinguisher. Unfortunately, they do not provide any method for estimation of some sources, which is critical for source separation of complex tissues. Additionally, quantitative weights are provided only for signature genes which number can vary for different sources, and can be as small as one gene. Authors do not apply their algorithm to complex mixtures as tumor transcriptome; they establish a proof of concept with in vitro mixtures of tissues.

The convex hull-based method does not require the independence of cell types assumption, nor the non-correlation assumption which can be interesting in the setup of closely related cell types. In theory, they also allow \(k>j\) (more sources than samples). So far, the existing tools are not directly applicable to tumor transcriptomes.

2.3.6 Matrix factorization methods

Matrix factorization is a general problem not specific to cell types deconvolution. It has been extensively used for signal processing (Zinovyev et al. 2013)and extraction of features from images (Hastie, Tibshirani, and Friedman 2009). Matrix factorization can also be called BSS or dimension reduction. Despite quite simple statistical bases they have been proven to be able to solve quite complex problems. Many matrix factorization methods can solve the problem of Eq. (2.1). They can solve it in different ways and concern different hypotheses.

Naturally, matrix factorization methods estimate simultaneously \(A\) and \(S\) matrices (cell proportions and profiles) given \(X\) rectangular matrix (genes \(\times\) samples) without any additional input.

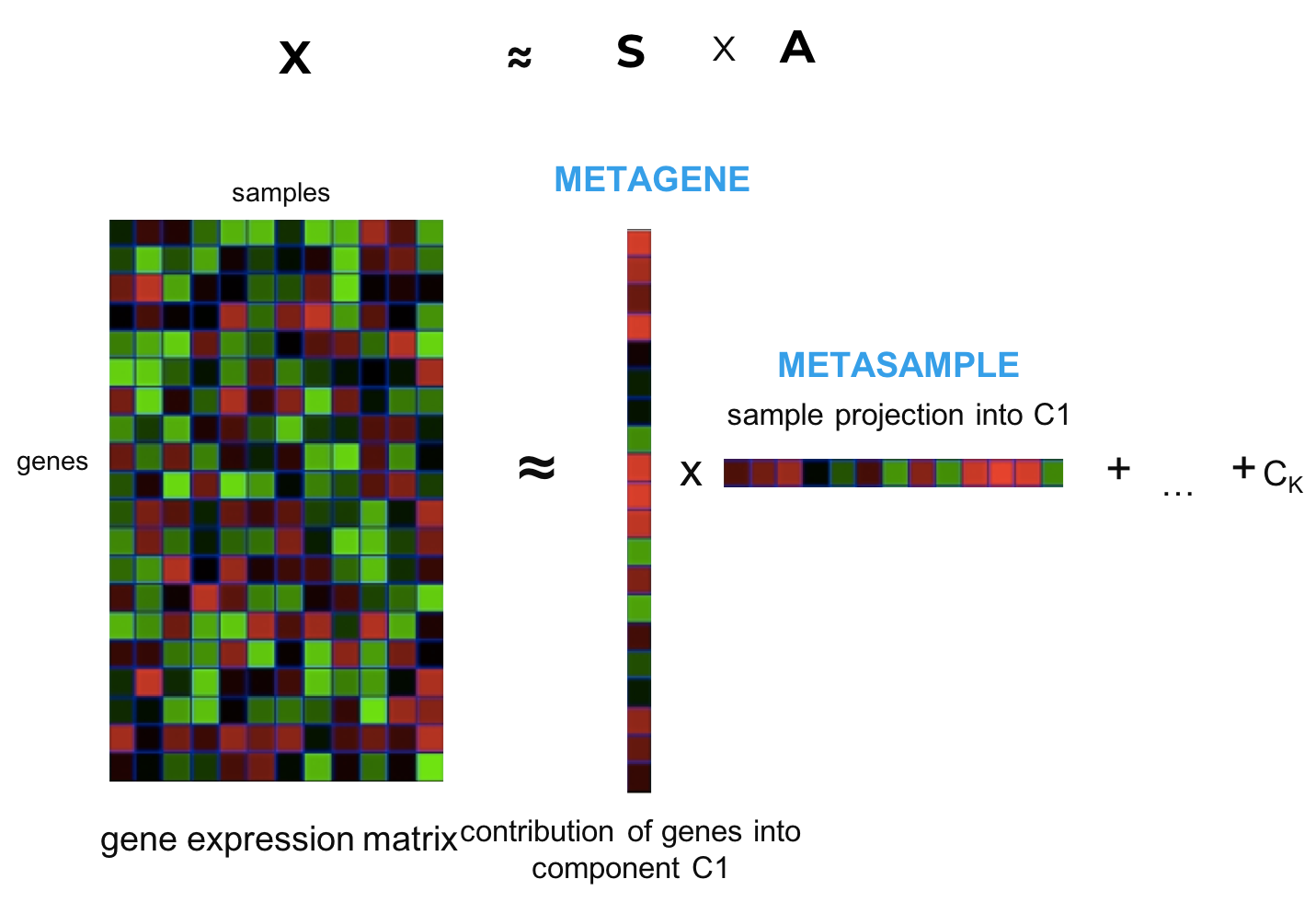
Figure 2.8: Principle of matrix factorisation of gene expression. The gene expression matrix \(X\) is decomposed into a set of metagenes \(S\) matrix and metasamples \(A\). Number of components C is defined with parametre \(k\).

2.3.6.1 Principal Components Analysis

One of the most popular methods, Principal Components Analysis (PCA) computes projections of the variables onto the space of the eigenvectors of the empirical covariance matrix, the projections are mutually uncorrelated and ordered in variance. The principal components provide a sequence of best linear approximations to that data.

PCA can be computed through eigen decomposition of the covariance matrix. Covariance matrix is computed as follows:

\[\begin{equation} \Sigma = \frac{1}{n-1}((X-\bar{x})^T(X-\bar{x})) \tag{2.16} \end{equation}\]

where \(\bar{x}\) is mean vector of the feature column in the data \(X\).

Then the matrix is decomposed to eigenvalues: \[\begin{equation} \mathbf{V^{-1}\Sigma V=D} \tag{2.17} \end{equation}\]

where \(\mathbf{V}\) is the matrix of eigenvectors and the \(\mathbf{D}\) diagonal matrix of eigenvalues.

It can be also computed using singular value decomposition (SVD) (computationally more efficient way):

\[\begin{equation} X= UDV^T \tag{2.18} \end{equation}\]

Here \(U\) is an \(N \times p\) orthogonal matrix (\(U^T U = I_p\)) whose columns \(u_j\) are called the left singular vectors; \(V\) is a \(p \times p\) orthogonal matrix (\(V^T V = I_p\)) with columns \(v_j\) called the right singular vectors, and \(D\) is a \(p \times p\) diagonal matrix, with diagonal elements \(d_1 \geq d_2 \geq ... \geq d_p \geq 0\) known as the singular values. The columns of \(UD\) are called the projections of principal components of \(X\) on axes.

PCA finds directions in which the samples are dispersed to define Principal Components. This dispersion is measured with variance, and resulting PCA components are variance-ordered.

As nicely described in (Rutledge and Jouan-Rimbaud Bouveresse 2013)

The first PC is the vector describing the direction of maximum sample dispersion. Each following PC describes the maximal remaining variability, with the additional constraint that it must be orthogonal to all the earlier PCs to avoid it contains any of the information already extracted from the data matrix. In other words, each PC extracts as much remaining variance from the data as possible. The calculated PCs are weighted sums of the original variables, the weights being elements of a so-called loadings vector. Inspection of these loadings vectors may help determine which original variables contribute most to this PC direction. However, PCs being mathematical constructs describing the directions of greatest dispersion of the samples, there is no reason for the loadings vectors to corresponding to underlying signals in the dataset. Most of the time, PCs are combinations of pure source signals and do not describe physical reality. For this reason, their interpretation can be fraught with danger.

Especially in the context of the cell-type deconvolution, it can imagine that different cell-types contribute to the variance, but one PC could explain the joint variance of many cell types.

Wang et al. (2015) used SVD to compute matrix inversion in order to separate tumor from the stroma. The method was applied to tumor transcriptomes and gives purity estimation quite different from other popular enrichment-based method ESTIMATE (Yoshihara et al. 2013).

Nelms et al. (2016) in CellMapper uses a semi-supervised approach based on SVD decomposition to dissect human brain bulk transcriptome. Authors define a query gene (a specific known gene), and then they decompose transcriptome into components (eigenvectors) and multiply by weights that are higher for the components correlated with the query gene. Then the matrix is transformed back to gene \(\times\) samples matrix, but query signal is amplified. The point is to find marker genes that characterize the same cell-type as the query gene. Authors did not aim at the identification of cell-type proportions or cell types profiles but identification of cell-type specific markers. They underline applicability of the method to rare cell types where many markers are not available. This approach was proposed by authors to be used to prioritize candidate genes in disease susceptibility loci identified by GWAS.

2.3.6.2 Non-negative matrix factorisation

Non-negative matrix factorization (Seung and Lee 1999) is an alternative approach to principal components analysis. It requires data are non-negative and it estimates components that are non-negative as well. It finds its application in image analysis and gene expression analysis where analyzed data are non-negative. The \(N \times p\) data matrix \(X\) is approximated by

\[X \approx WH \]

where \(W\) is \(N \times r\) and \(H\) is \(r \times p\), \(r ≤ max(N,p)\). We assume that \(x_{ij}\) ,\(w_{ik}\), \(h_{kj}\)\(\geq 0\).

Which is a special case of Eq. (2.1).

The matrices \(W\) and \(H\) are found by maximizing \[\begin{equation} \mathcal{L}(W, H) = \sum^N_{i=1}\sum^{p}_{j=1}[x_{ij} log(WH)_{ij} − (WH)_{ij} ] \tag{2.19} \end{equation}\]

The log-likelihood from a model in which \(x_{ij}\) is drawn from a pre-defined distribution (i.e., Poisson) with a mean \((WH)_{ij}\).

This formula can be maximized through minimization of divergence:

\[\begin{equation} \underset{W,H}{min} f(W,H) = \frac{1}{2}\rVert X-WH\rVert^2_F \tag{2.20} \end{equation}\]

Where \(\rVert .\rVert_F\) is Frobenius norm, which can be replaced by Kullback-Leibler divergence.

The optimization can be done employing different methods:

• euclidean update with multiplicative update rules, it is the classic NMF (Seung and Lee 1999) \[ W \leftarrow W \frac{XH^T}{WHH^T}\\H \leftarrow H\frac{W^TX}{W^TWH} \tag{2.21} \]
• alternating least squares (Paatero and Tapper 1994) where the matrices W and H are fixed alternatively
• alternating non-negative least squares using projected gradients (Lin (2007))
• convex-NMF (Ding, Tao Li, and Jordan 2010) imposes a constraint that the columns of \(W\) must lie within the column space of \(X\), i.e. \(W = XA\) (where \(A\) is an auxiliary adaptative weight matrix that fully determines \(W\)), so that \(X=XAH\). In this method only \(H\) must be non-negative.

The NMF algorithms can differ in initialization method as well and even in situations where \(X = WH\) holds exactly, and the decomposition may not be unique. This implies that the solution found by NMF depends on the starting values. The performance of different combinations applied to MRS data from human brain tumors can be found in Ortega-Martorell et al. (2012).

Brunet et al. (2004) created an NMF Matlab toolbox and demonstrated applicability of NMF (using Kullback-Leibler divergence and euclidean multiplicative update (Lee and Seung 2000) to cancer transcriptomes with focus on cancer subtyping (focusing on the \(H\) matrix). Brunet et al. (2004) also proposed a way to evaluate the optimal number of factors (sources) to which matrix should be decomposed.

NMF as imposing non-negativity in the context of decomposition of transcriptomes seems as an attractive concept as both cell profiles and cell proportions should be non-negative. It is not surprising then that some authors used NMF to perform cell-type deconvolution.

To my knowledge, deconf (Repsilber et al. 2010) was the first tool proposing NMF cell-type deconvolution of PBMC transcriptome, of considerable dimensions, 80 samples (40 control and 40 cases) of Tuberculosis. Repsilber et al. (2010) employed random initialization and alternating non-negative least squares to minimize the model divergence. The complete deconvolution of the transcriptome was used to perform DEG analysis on the deconvoluted profiles.

Shen-Orr and Gaujoux (2013), not only presented exhaustive literature review through implementing cell-type deconvolution methods in an R package CellMix (Gaujoux and Seoighe 2013) but also proposed a semi-supervised NMF for cell-type deconvolution and published an R package implementing different NMF methods (Gaujoux and Seoighe 2010). The semi-supervised version of NMF proposed by Gaujoux and Seoighe (2013), need a set of specific marker genes for each desired cell type. Then at initialization and after each iteration of the chosen NMF algorithm (applies to some versions of NMF (Seung and Lee 1999; Brunet et al. 2004; Pascual-Montano et al. 2006), “each cell type signature has the values corresponding to markers of other cell types set to zero. The values for its own markers are left free to be updated by the algorithm’s own iterative schema”. Applying their algorithm to in vitro controlled dataset [GSE11058 (Abbas et al. 2009), testing selected NMF implementations and a varying number of markers per cell, authors observed the best performance with guided version of brunet (Brunet et al. 2004) implementation.

Moffitt et al. (2015) applied NMF to separate tumor from stroma in pancreatic ductal carcinoma (PDAC) using multiplicative update NMF. They scaled \(H\) matrix rows to 1 so that the values correspond to the proportions. Authors tested different possibilities of the number of sources (\(k\)), the final number of factors was defined through hierarchical clustering on gene-by-gene consensus matrix of top 50 genes of each component.

Finally Liu et al. (2017) proposed post-modified NMF in order to separate in vitro mixtures of different tissues.

In brief, NMF is a popular, in biology, algorithm performing source separation with non-negativity constraint. It was applied to in vitro cell-mixtures and blood transcriptomes, showing a satisfying accuracy of cell-type in silico dissection and evaluating proportions. It was also applied in cancer context. However, it did not recover cell-type specific signals but rather groups of signals that could be associated with cancer or stroma.

2.3.6.3 Independent Components Analysis

Independent Components Analysis is written as in Eq. (2.1) maximizing independence and non-Gaussianity of columns of \(S\): \(S_i\). It was first formulated by Herault and Jutten (1986)

The independence can be measured with entropy, kurtosis, mutual information or negentropy measure \(J(Y_j )\) (Hyvärinen and Oja 2000) defined by

\[\begin{equation} J(Y_j ) = H(Z_j ) - H(Y_j ) \tag{2.22} \end{equation}\]

where \(H(Y_j )\) is entropy, \(Z_j\) is a Gaussian random variable with the same variance as \(Y_j\). Negentropy is non-negative and measures the deviation of \(Y_j\) from Gaussianity. An approximation of negentropy is used in popular implementation of FastICA (Hyvärinen and Oja 2000). Other existing implementations of ICA are

• Infomax (Bell and Sejnowski 1995) using Information-Maximization that maximizes the joint entropy
• JADE (Cardoso and Souloumiac (1993)) on the construction of a fourth-order cumulants array from the data

However, they are usually a lot slower which limits their application to a large corpus of data and Teschendorff et al. (2007) demonstrated that FastICA gives the most interpretable results.

Therefore, I will focus on FastICA implementation as it will be extensively used in the Results part.

FastICA requires prewhitening of the data (centering and whitening). Centering is removing mean from each row of \(X\) (input data). Whitening is a linear transformation that columns are not correlated and have variance equal to 1.

Prewhitenning

1. Data centering \[\begin{equation} x_{ij} \leftarrow x_{ij} - {\frac {1}{M}}\sum_{j^{\prime }}x_{ij^{\prime }} \tag{2.23} \end{equation}\] \(x_{ij}\): data point
2. Whitenning \[\begin{equation} \mathbf {X} \leftarrow \mathbf {E}\mathbf {D} ^{-\frac{1}{2}}\mathbf {E} ^{T}\mathbf {X} \tag{2.24} \end{equation}\] Where \(\mathbf {X}\) - centered data, \(\mathbf {E}\) is the matrix of eigenvectors, \(\mathbf{D}\) is the diagonal matrix of eigenvalues

Algorithm 1: FastICA multiple component extraction

INPUT: \(K\) Number of desired components

INPUT: \(X \in \mathbb{R}^{N \times M}\) Prewhitened matrix, where each column represents an \(N\)-dimensional sample, where \(K \leq N\)

OUTPUT: \(A \in \mathbb{R}^{N \times K}\) Un-mixing matrix where each column projects \(\mathbf {X}\) onto independent component.

OUTPUT: \(S \in \mathbb{R}^{K \times M}\) Independent components matrix, with \(M\) columns representing a sample with \(K\) dimensions.

\[\begin{equation} \tag{2.25} \end{equation}\] For \(p\gets [1, K]\)

\(\mathbf{w}_{p} \gets\) Random vector of length \(N\)

WHILE \(\mathbf{w_{p}}\) changes

       \(\mathbf{w}_p \gets \frac{1}{M}Xg(\mathbf{w}_p^TX)^T - \frac{1}{M}g'(\mathbf{w}_p^TX)1w_p\)

       \(\mathbf{w}_p \gets \mathbf{w}_p - (\sum_{j=1}^{p-1}\mathbf{w}_p^T\mathbf{w}_j\mathbf{w}_j^T)^T\)

       \(\mathbf{w}_p \gets \frac{\mathbf{w}_p}{\lVert \mathbf{w}_p \rVert}\)

where \(\mathbf {1}\) is a column vector of 1’s of dimension \(M\)

OUTPUT: \(A = [\mathbf{w}_1, ..., \mathbf{w}_K]\)

OUTPUT: \(S = \mathbf{A}^T\mathbf{X}\)

However, the results of this algorithm (Alg. 1. (2.25)) are not deterministic, as the \(\mathbf{w}_{p}\) initial vector of weights is generated at random in the iterations of fastICA. If ICA is run multiple times, one can measure stability of a component. Stability of an independent component, regarding varying the initial starts of the ICA algorithm, is a measure of internal compactness of a cluster of matched independent components produced in multiple ICA runs for the same dataset and with the same parameter set but with random initialization (Himberg and Hyvarinen, n.d.).

The Icasso procedure can be summarized in a few steps :

1. applying multiple runs of ICA with different initializations
2. clustering the resulting components
3. defining the final result as cluster centroids
4. estimating the compactness of the clusters

In brief, ICA looks for a sequence of orthogonal projections such that the projected data look as far from Gaussian as possible. ICA starts from a factor analysis solution and looks for rotations that lead to independent components.

So far, ICA was used to deconvolute transcriptomes into biological functions (Biton et al. 2014; Engreitz et al. 2010; Gorban 2007; Teschendorff et al. 2007; Zinovyev et al. 2013). However, it has never been used for cell-type deconvolution.

In theory, ICA outputs: \(S\) could be interpreted as sources and \(A\) as proportions in the cell-type deconvolution context. In practice, the fact that the ICA allows negative weights of projections, it makes the interpretation less trivial.

To my knowledge, my DeconICA R-package (that will be described in the results part) is the first method allowing interpretation of ICA-based signals as cell-type context-specific signatures and quantify their abundance in the transcriptome.

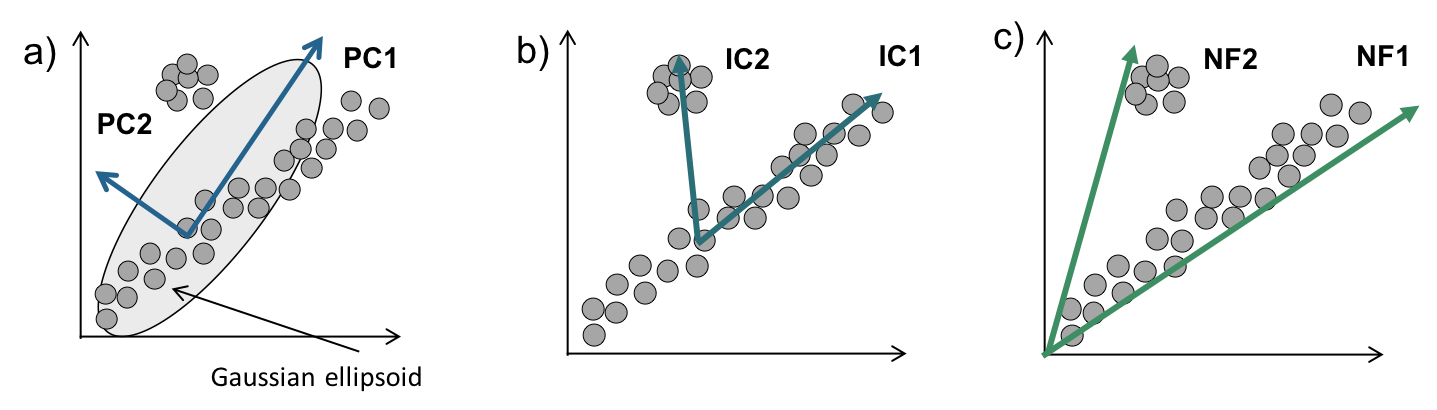
Figure 2.9: Simple illustration of matrix factorisation methods. Adapted with permision from (Zinovyev et al. 2013)

All in all, matrix factorization methods are able to decompose a gene expression matrix into a weighted set of genes (metagene)(\(S\)) and weighted set of samples (metasample \(A\)). Discussed here PCA, NMF and ICA differ in constraints and starting hypotheses. PCA components are ordered by variance and are orthogonal in the initial space of data (Fig. 2.9 ). NMF impose non-negativity constraint and ICA independence of sources hypothesis. Components of NMF and ICA are not ordered. For all the matrix factorization methods number of components (or factors) (\(k\)) needs to be given to the algorithm. Some authors propose a way to estimate the optimal number of components usually justified in a specific context. NMF and SVD were applied in the context of cell-type deconvolution while ICA, so far, was used to dissect transcriptome into factors related to signaling pathways, technical biases or clinical features. Also, ICA was proven to find reproducible signals between different datasets (Cantini, Kairov, et al. 2018; Teschendorff et al. 2007). I am going to discuss this aspect of the Results section.

2.3.7 Attractor metagenes

A method proposed by Cheng, Yang, and Anastassiou (2013) that can be run in semi-supervised or unsupervised mode is called attractor metagenes. Authors describe their rationale as follows:

We can first define a consensus metagene from the average expression levels of all genes in the cluster, and rank all the individual genes in terms of their association (defined numerically by some form of correlation) with that metagene. We can then replace the member genes of the cluster with an equal number of the top-ranked genes. Some of the original genes may naturally remain as members of the cluster, but some may be replaced, as this process will “attract” some other genes that are more strongly correlated with the cluster. We can now define a new metagene defined by the average expression levels of the genes in the newly defined cluster, and re-rank all the individual genes concerning their association with that new metagene; and so on. It is intuitively reasonable to expect that this iterative process will eventually converge to a cluster that contains precisely the genes that are most associated with the metagene of the same cluster so that any other individual genes will be less strongly associated with the metagene. We can think of this particular cluster defined by the convergence of this iterative process as an “attractor,” i.e., a module of co-expressed genes to which many other gene sets with close but not identical membership will converge using the same computational methodology.

Which in pseudocode works as described in Algorithm 2 (2.26) and it is implemented in R code is available online in Synapse portal.

Algorithm 2: Attractor metagenes algorithm

INPUT: \(\alpha\) shrinkage parameter

INPUT: \(X \in \mathbb{R}^{N \times M}\) gene expression matrix

OUTPUT: \(m_j\) metagene of \(g_{seed}\)

\[\begin{equation} \tag{2.26} \end{equation}\]

\(g_{seed} \gets\) a gene from \(1:N\)

\(I^{\alpha}(g_{seed}; g_i)\) # compute association beteen \(g_{seed}\) and \(g_i\)

\(w_i = f(I^{\alpha}(g_{seed}; g_i))\) # compute weights for each gene

\(m_0 = \frac{\sum^N-1_{i=1}(g_iw_i)}{\sum^N-1_{i=1}w_i}\) # compute metagene as weighted average of all genes

\(I^{\alpha}(m_0; g_i)\) # compute association between metagene \(m_0\) and each gene \(g_i\)

REPEAT

       \(w_i = f(I^{\alpha}(m_0; g_i))\)

       \(m_j = \frac{\sum^N-1_{i=1}(m_0w_i)}{\sum^N-1_{i=1}w_i}\)

UNTIL \(m_{j+1} = m_j\)

The produced signatures’ weights are non-negative. In the original paper, the generation of tumor signatures leads to three reproducible signatures among different tumor types, including leucocyte metagene. Typically with the essential parameter \(\alpha=5\), they discovered typically approximately 50 to 150 resulting attractors.

This method was further to study breast cancer (Al-Ejeh et al. 2014) and to SNP data (Elmas et al. 2016).

There is a possibility to tune the \(\alpha\) parameter in order to obtain more or less metagenes that would be possibly interpretable as cell-type signatures.

2.3.8 Others aspects

Here I will discuss transversal aspects common to most deconvolution methods. They play the critical role in the final results and are often omitted while algorithms are published which impacts the reproducibility significantly.

2.3.8.1 Types of biological reference

Let us consider the case of the deconvolution where neither \(A\) or \(S\) are not known (Eq. (2.1)) (as in the case of cancer transcriptomes), and we would like to estimate cell proportions or both cell proportions and cell profiles. No matter if the method is supervised or unsupervised at some point of the protocol the biological knowledge about cell types is necessary in order to either derive the model or interpret the data. I discussed signatures from the biological perspective in Section 1.3.3. Here, I would like to stress the importance of the design of gene signatures which aim is to facilitate cell-type deconvolution.

Depending on chosen solution different type of reference can be used. In regression algorithms, a way to approximate the individual cell-type profiles is necessary to estimate proportions. However, the genes that are the most variant between cell types are enough for regression, and not all profiles are necessary. A matrix containing gene expression characteristic for a set of cell-types, often for selected, most discriminative, genes is called basis matrix. The choice of the genes and the number of the genes impact the outcome (Vallania et al. 2017) significantly. Therefore, most of the regression methods come together with a new basis matrix, ranging from hundreds to tens of genes. Typically, genes selected for basis matrix should be cell-type specific in respect to other estimated cell types, validated across many biological conditions (Hoffmann et al. 2006). Racle et al. (2017) adds a weight directly in the regression formula (see Eq. (2.9) ) that corresponds to the variability of a signature gene between independent measurements of the same cell type so that the least inter-cell type variable genes have more weight in the model. CellMix (Gaujoux and Seoighe 2013) regroups different indexes to select the most specific genes based on signal-to-noise ratio. However, the most popular method is the selection of differentially expressed genes between pure populations. Often criteria for the optimal number of genes in the basis matrix are not knowledge-based but data-driven. Abbas et al. (2009) uses matrix mathematical property - condition number of basis matrix (kappa) in order to select the number of genes. CIBERSORT and many other regression methods follow the same approach. Newman et al. (2015) also added another step while constructing the basis matrix, and it preselects reference profiles having maximal discriminatory power. Some authors (Ju et al. 2013; Nelms et al. 2016) propose to find marker genes through correlation with a provided marker gene (a single one or a group of genes).

In enrichment methods, gene list can be enough to estimate cell abundance, sometimes (i.e., GSEA) ranked gene list is necessary. The choice of extremely specific markers is crucial for accurate call-type abundance estimation. The choice of markers can also be platform-dependent, this point is strongly underlined in (Becht et al. 2016). An interesting possibility is the use of gene list of different cell states in order obtain coarse-grain resolution.

The impact of missing gene from a signature in the bulk dataset remains an unanswered question. It would be logical that shorter the gene list for a specific cell, a lack of a gene can have more impact on the result. There is a need for an accurate threshold between robustness and accuracy of the method.

In unsupervised methods, purified cell-profiles, signatures or list of genes can be used a posteriori to interpret the obtained sources. Even though the choice of reference does not affect the original deconvolution, it affects the interpretation. The advantage of a posteriori interpretation is a possibility to use different sources and types of signatures in order to provide the most plausible interpretation. It is common that the way of interpretation of components is not included in the deconvolution tool (Wang et al. 2016, Newberg et al. (2018), Moffitt et al. (2015)), even though it is a crucial part of the analysis.

For the deconvolution of tumoral biopsies, most of the reference profiles, up to now, are coming from the blood, which is the most available resource. Therefore most of the methods make a hypothesis that blood cell-type profiles/signatures are a correct approximation of cancer infiltrating immune cells. Rare models like PERT (Qiao et al. 2012) or ImmuneStates (Vallania et al. 2017) discuss the perturbation of the blood-derived profiles in diseases.

With the availability of single-cell RNA-seq of human cancers (Chung et al. 2017; Lavin et al. 2017; Li, Liu, and Liu 2017; Puram et al. 2017; Schelker et al. 2017; Tirosh et al. 2016; Zheng et al. 2017), we gain more knowledge on immune cells in TME, and there is growing evidence that they differ importantly from blood immune cells. Racle et al. (2017) show that lymph node-resident immune cells have expression profile closer to blood immune cells than cancer immune cells. Schelker et al. (2017) shows, using a synthetic bulk dataset that using single cell profiles with existing regression methods (CIBERSORT) can improve their performance in the cancer context. However, availability of scRNA-seq remains succinct and probably do not embrace the patient heterogeneity that can be found in large bulk transcriptome cohorts.

2.3.8.2 Data processing

Data pre- and post-processing can have a substantial impact on the deconvolution. Many authors apply strong filtering of genes (Wang et al. 2016), removing probes with the lowest and the highest expression (potential outliers). In many cases, data preprocessing is not detailed and therefore impossible to reproduce.

There is also a debate on the data normalization.

In microarray analysis pipeline, data are transformed into log-space, usually \(log_2(x+1)\) in order to make the distribution closer to Gaussian and therefore facilitate statistical hypothesis testing (Hoyle et al. 2002). It also stabilizes the variance (Tsai, Chen, and Chen 2003).

Most of the authors suggest to use counts (not transformed into log-space) for estimating cell abundance as log-transformed data violate the linearity assumption (Zhong et al. 2013), some opt against it (Shannon et al. 2017; Clarke, Seo, and Clarke 2010), and some envisage both possibilities (Erkkilä et al. 2010; Repsilber et al. 2010).

For the RNA-seq data TPM (transcripts per million) normalization is preferred or even required by most methods (Chen et al. 2018; Finotello et al. 2017; Racle et al. 2017). Jin, Wan, and Liu (2017) performed an extensive analysis of RNA-seq data processing that preserves best the linearity for deconvolution suggesting that TPM normalization for deconvolution studies.

For matrix factorization: PCA, ICA the data are usually log-transformed and centred to reduce the influence of extreme values or outliers. NMF for cell-type deconvolution is usually applied in non-log space.

2.3.8.3 Validation

Most of algorithm validation starts with in silico mixtures (Fig. 2.10). In published articles, the bulk transcriptome is simulated in two ways (1) mixing numerically simulated sources at defined proportions of given distribution (i.e. uniform) using linear model (for instance NMF) (2) using sampling (for instance Monte Carlo) to randomly select existing pure profiles and mixing them (additive model) at random proportions. To the obtained bulk samples, noise can be added at different steps of the simulation. Additional parameters can be defined in in silico mixtures, for instance, CellMix allows defining the number of marker genes (specific to only one source) for each cell type. The simulated benchmark based on single cell data was used in Schelker et al. (2017) and Görtler et al. (2018). In this framework, simulated data was obtained through summing single cell profiles at known proportions. The main pitfall of those methods is that in the proposed simulations the gene covariance structure is not preserved. In reality, the proportions of cell types are usually not random, and some immune cell types can be correlated or anti-correlated. In addition, these simulations create a simple additive model which perfectly agrees with the linear deconvolution model. This is probably not the case of the real bulk data affected by different factors as cell cycle, technical biases, patients heterogeneity and especially cell-cell interactions.

Figure 2.10: From theory to practice: a simplified pipeline of model validation. The scheme reflects pipeline of data validation commonly used in transcriptome deconvolution methods validation. The project can be started from a biological problem (A) and then a way to solve the problem in mathematical model (C) is tested. Most commonly, the project starts with the model (C) then it is tested on simulated data (D). Next level of difficulty is testing the model with real data, so-called, benchmark data (B) that were generated in some biological context different from initial problem. They need to be usually normalized (E) before the model is challenged. B data are widely used as they are easily available and there is some validation available facilitating comparison. Lastly, it is assumed that if the method works fine in the context B, it will work as well in the context A, preferably accompanied by some partial validation. One can replace A by cancer transcriptomics, B by blood data or in vitro mixtures if the focus is TME bulk transcriptomics deconvolution.

Naturally, algorithms validated with simulated mixtures are then validated with controlled in vitro mixtures of cell types or tissues mixed in known proportions. The most popular benchmark datasets are:

• mix of human cell lines Jurkat, THP-1, IM-9 and Raji in four different concentration in triplicates and the pure cell-line profiles (GSE11058) (Abbas et al. 2009);
• mix of rat tissues: liver, brain, lung mixed in 11 different concentrations in triplicates and the pure tissues expression(GSE19830) (Shen-Orr et al. 2010)

Similar simple mixtures are also proposed by other authors (Becht et al. 2016, Kuhn et al. (2011)). This type of benchmark adds the complexity of possible data processing and experimental noise. However, it still follows an almost perfect additive model as the cell/tissues do not interact and they are only constituents of the mixture.

Several tools performed systematic benchmark using PBMC or whole blood datasets, where for a number of patients (that can be over one hundred) FACS measured proportions of selected cell types and bulk transcriptomes are available. Many such datasets can be found at IMMPORT database. Aran, Hu, and Butte (2017) kindly shared with scientific community two datasets with a considerable number of patients (\(\sim80\) and \(\sim110\)) and processed FACS data (actual proportions) on their github repository. It is still important to remember that liquid tissues are easier to deconvolute and for the tools using a priori reference, the reference profiles are obtained from the blood. Therefore the context remains consistent.

For the solid cancer tissues deconvolution, some of the tools were validated with the stained histopathology cuts using in situ-hybridisation (ISH) (Kuhn et al. 2011) or immunohistochemistry (IHC) (Becht et al. (2016)). Often this method estimates a limited number of cell types and the measured abundance of pictures can also be biased by the technical issues (image/ staining quality).

Authors of EPIC validated their tool with paired RNAseq and Lymph node FACS-derived proportions in 4 patients (GSE93722). They also noticed that it is more straightforward to correctly evaluate lymph node immune cell types than cancer infiltrating cell types as lymph node-resident cells are more similar to the blood immune cells.

FACS and gene expression of blood cancer (Follicular lymphoma) were also used by Newman et al. (2015) for 14 patients (unpublished data). For solid tissues, Newman et al. (2015) used paired FACS and expression datasets of normal lung tissues for B-cell and CD8 and CD4 T cells of 11 patients (unpublished data).

Some authors proposed to cross-validate estimated proportions with estimated proportions based on a different data input (i.e., methylome) (Li et al. 2016, Şenbabaoğlu et al. (2016)) or CNA (Şenbabaoğlu et al. (2016)). This type of validation is interesting, even though in many projects only one type of data types are available for the same samples. TCGA data is one of few exceptions.

Finally, a validation of deconvolution of solid cancer tissues remains incomplete as no paired expression and FACS data is available up to date.

2.3.8.4 Statistical significance

A little number of tools propose a statistical significance assessment. CIBERSORT computes empirical p-values using Monte Carlo sampling. Infino authors (Zaslavsky et al. 2017) provide a confidence interval for the proportion estimations. This allows knowing which proportion estimation are more trustful than other.

Most tools compare themselves to others measuring the accuracy of the prediction, or Pearson correlation, on the benchmark datasets (described above). Often, in the idealized mixtures, methods perform well. Evaluation of their performance in cancer tissues remains unanswered without proper statistical evaluation.

2.3.9 Summary

The field of computational transcriptome deconvolution is continuously growing. Initially used to solve simple in vitro or simulated mixtures of quite distinct ingredients, then to deconvolute blood expression data, finally applied to solid cancer tissues. In cancer research, digital quantification of cancer purity becomes a routine part of big cancer research projects (Yoshihara et al. 2013). Cell-type quantification, even though the validation framework and statistical significance of deconvolution tools can still be improved, seems to be considered as a popular part of an analytical pipeline of bulk tumor transcriptomes (Cieślik and Chinnaiyan 2017). Different types of approaches try to solve the deconvolution problem, focusing on different aspects of the quantification, or proposing methodologically different approaches. Methods proposing an unsupervised solution to the deconvolution problem of transcriptomes are still underrepresented. All the tools assume a linear additive model without explicitly including the impact of possible interactions on the cell-type quantification. The tools that met the most prominent success were proven by the authors to be readily applicable to a variety of cancer datasets and reusable without an extra effort (through a programming library or web interface). The field is still waiting for a gold standard validation benchmark that would allow a fair comparison of all the tools in solid cancer tissues. It is also remarkable that the recent methods focus on quantification of the abundance of an average representation of cell-types without aspiring to deconvolute the cell-type context-specific profiles. Thanks to various cancer single-cell data and big-scale projects (Regev et al. 2017), we will be able to improve the existing deconvolution approaches and finally replace the collection of bulk transcriptomes by a collection of scRNA-seq ones.

2.4 Deconvolution of other data types

The transcriptome data is not the unique omic data type that can be used to infer cell type proportions. Genomic and epigenomic data was used in numerous publications to perform cell-type deconvolution or estimate sample purity. I will present a general landscape of the tools and methods used for this purpose.

2.4.1 DNA methylation data

Cell-type composition can be computed from DNA methylation data (described in Section X). In EWAS (Epigenome Wide Association Studies) variation origination from cell types is considered as an important confounding factor that should be removed before comparing cases and controls and defining Differentially Methylated Positions (DMPs). Teschendorff and Zheng (2017) reviewed ten tools for epigenome deconvolution. Authors identify six of the described methods as reference-free (which I called in this Chapter unsupervised), three are regression-based, and one is semi-supervised. Another review on this topic was authored by Titus et al. (2017).

Unsupervised methods employed in methylome cell-type deconvolution are RefFreeEWAS (Houseman, Molitor, and Marsit 2014), SVA (Leek and Storey 2007) are based on SVD, ISVA based on ICA [Teschendorff, Zhuang, and Widschwendter (2011)) are more general methods that aim to detect and remove confounders from the data (that do not need to be necessary the cell types). RUVm (Maksimovic et al. 2015) is a semi-supervised method using generalized least squares (GLS) regression with negative reference also used to remove unwanted variation from the data and could be potentially adapted to cell-type deconvolution. EWASher (Zou et al. (2014)) is linear mixed model and PCA based method that corrects for cell-type composition. Similarly, ReFACTor (Rahmani et al. 2016) use sparse PCA to remove the variation due to cell-type proportions. Houseman et al. (2016) proposed RefFreeCellMix: an NMF model with convex constraints to estimate factors representing cell types and cell-type proportions and a likelihood-based method of estimating the underlying dimensionality (\(k\) number of factors). A different tool MeDeCom (Lutsik et al. 2017) uses alternating non-negative least squares to fit a convex hull.

As far as supervised methods are concerned, EPiDISH (Epigenetic Dissection of Intra-Sample-Heterogeneity) R-package (Teschendorff and Zheng 2017) includes previously published tools: Quadratic programming method using reference specific DNAse hypersensitive sites [Constrained Projection (CP) (Houseman et al. 2012)), adapted to methylome deconvolution CIBERSORT algorithm (\(\nu\)-SVR) and robust partial correlations (RPC) method (a form of linear regression). Reference cell-type specific profiles were obtained from the blood.

eFORGE (Breeze et al. 2016) can detect in a list of DMPs if there is a significant cell-type effect.

EDec (Onuchic et al. 2016) uses DNAm to infer factors proportions using NMF and then derives factors profiles though linear regression of transcriptome data of cancer datasets. Authors identify the tumor and stroma compartments and profiles. However, they admit the error rate for profiles is quite high for most genes.

Wen et al. (2016) focused on intra-tumor heterogeneity (clonal evolution) based on DNAm data. Profiles obtained from cell lines were used in a regression model to identify the proportions of sub-clones in breast cancer data. InfiniumPurify (Zheng et al. 2017) and LUMP (Aran, Sirota, and Butte 2015) uses DNAm to estimate sample purity.

The validation framework for methylation deconvolution is very similar to transcriptome ones: in silico mixtures and FACS-measured proportions of the blood. Most of the tools assume the cell composition is a factor the most contributing to the variability and therefore SVD/PCA based approaches are sufficient to correct for the variability. According to Teschendorff and Zheng (2017), this assumption was not proven to hold true in solid tissues like cancer. Supervised methods have the same drawback as in the case of the transcriptome, and they use purified profiles from one context to derive cell proportions in a different context. In overall, it seems that no study proposed cell-type quantification based on methylome profiles in a pan-cancer manner.

2.4.2 Copy number aberrations (CNA)

To my knowledge there is no method using CNA data in order to estimate cell-type composition, as CNA occur in tumor tissue and natural distinction can be made between tumor and normal cells and within tumor cells (intra-tumor).

Therefore, copy number aberrations can be used to estimate tumor purity and clonality. BACOM 2.0 (Fu et al. 2015), ABSOLUTE (Carter et al. 2012), CloneCNA (Yu, Li, and Wang 2016), PureBayes (Larson and Fridley 2013), CHAT (Li and Li 2014), ThetA (Oesper, Mahmoody, and Raphael 2013), SciClone (Miller et al. 2014), Canopy (Jiang et al. 2016), PyClone (Roth et al. 2014), EXPANDS (Andor et al. 2014) estimate tumor purity and quantify true copy numbers. OmicTools website reports 70 tools serving this purpose and their review goes beyond the scope of my work. Most tools use tumor and normal samples, paired if possible. QuantumClone seem to be the only tool that requires a few samples from the same tumor (in time or space dimension).

Aran, Sirota, and Butte (2015) published Consensus measurement of purity estimation that combines purity estimations based on different data types (available in cBioportal) using: ESTIMATE (Yoshihara et al. 2013) (gene expression data), ABSOLUTE (Carter et al. 2012) (CNA), LUMP (Aran, Sirota, and Butte 2015) (DNAm and IHC of stained slides. Authors concluded that the estimation based on different data types highly correlate with each other, besides the IHC estimates, which suggests that IHC provides a qualitative estimation of purity.

2.5 Summary of the chapter

A plethora of machine learning solutions has been developed to solve problems of different nature. Supervised and Unsupervised approaches can be distinguished depending if a model is provided a set of training data with known response or the algorithm works blindly trying to find patterns in the data. Some of the algorithms found an essential application in healthcare and are included in the clinical routine.

One of the critical problems that can, in theory, be solved with ML, is bulk omic data deconvolution. Different types of deconvolution of cancer samples can be distinguished: clonal, purity and cell-type deconvolution. Here I focused on cell-type deconvolution of transcriptome data. Through an extensive review, I presented 64 tools and divided them into categories depending on the adapted type of approach. I distinguished probabilistic, enrichment-based, regression-based, convex hull, matrix factorization and attractor metagene approaches that can be used for cell-type deconvolution. I detailed the basis of the different models and highlighted the most important features counting for cell-type deconvolution.

DNAm data were also used to estimate cell-type proportions. However, the heterogeneity found in methylome data resulting from the difference in cell type proportions is usually seen as a confounding factor to be removed. CNA data can be used for estimation of tumor purity and clonality.

In brief, for the transcriptome cell-type deconvolution, it can be observed that just a limited number of tools are usable in practice in order to deconvolute large cancer cohorts and without the need to provide hard to estimate parameters. Supervised methods applied to cancer use reference-profiles coming from a different context. Unsupervised tools, so far, are somewhat underrepresented in the field and do not offer a solution directly applicable to cancer transcriptomes of high dimensions. All of the presented methods are still waiting for consistent validation with the gold standard benchmark. This could be done if systematic data of bulk transcriptome paired with FACS-measured cell-type proportions information for many cells and in many samples were generated. Another unanswered question is the validity of the linear mixture model in the presence of cell-cell interactions.

There is still a room for improvement in the field in order to provide more user-friendly, accurate and precise cell-type abundance estimations.

A question can be asked, are cell-type proportions enough to understand tumor immune phenotypes? Can we extract more valuable information from the bulk omic data that would give useful insight to biological functions of the in silico dissected cells?

References

Mitchell, Tom M. (Tom Michael). 1997. Machine Learning. McGraw-Hill.

Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. 2009. The Elements of Statistical Learning. Springer Series in Statistics. New York, NY: Springer New York. doi:10.1007/978-0-387-84858-7.

Xu, Rui, and Donald C. Wunsch. 2008. Clustering. Hoboken, NJ, USA: John Wiley & Sons, Inc. doi:10.1002/9780470382776.

Van Der Maaten, Laurens, and Geoffrey Hinton. 2008. “Visualizing Data using t-SNE.” J. Mach. Learn. Res. 9: 2579–2605. https://lvdmaaten.github.io/publications/papers/JMLR{\_}2008.pdf.

Mcinnes, Leland, and John Healy. 2018. “UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction.” https://arxiv.org/pdf/1802.03426.pdf.

Becht, Etienne, Charles-Antoine Dutertre, Immanuel W.H. Kwok, Lai Guan Ng, Florent Ginhoux, and Evan W Newell. 2018. “Evaluation of UMAP as an alternative to t-SNE for single-cell data.” bioRxiv. Cold Spring Harbor Laboratory, 298430. doi:10.1101/298430.

“deconvolution | Definition of deconvolution in English by Oxford Dictionaries.” 2018. Accessed July 3. https://en.oxforddictionaries.com/definition/deconvolution.

Cherry, E. Colin. 1953. “Some Experiments on the Recognition of Speech, with One and with Two Ears.” J. Acoust. Soc. Am. 25 (5). Acoustical Society of America: 975–79. doi:10.1121/1.1907229.

Shen-Orr, Shai S, and Renaud Gaujoux. 2013. “Computational deconvolution: extracting cell type-specific information from heterogeneous samples.” Curr. Opin. Immunol. 25 (5): 571–78. doi:10.1016/j.coi.2013.09.015.

Schwartz, Russell, and Stanley E Shackney. 2010. “Applying unmixing to gene expression data for tumor phylogeny inference.” BMC Bioinformatics 11 (1). BioMed Central: 42. doi:10.1186/1471-2105-11-42.

Venet, D, F Pecasse, C Maenhaut, and H Bersini. 2001. “Separation of samples into their constituents using gene expression data.” Bioinformatics 17 Suppl 1: S279–87. http://www.ncbi.nlm.nih.gov/pubmed/11473019.

Abbas, Alexander R., Kristen Wolslegel, Dhaya Seshasayee, Zora Modrusan, and Hilary F. Clark. 2009. “Deconvolution of Blood Microarray Data Identifies Cellular Activation Patterns in Systemic Lupus Erythematosus.” Edited by Patrick Tan. PLoS One 4 (7). Public Library of Science: e6098. doi:10.1371/journal.pone.0006098.

Newman, Aaron M, Chih Long Liu, Michael R Green, Andrew J Gentles, Weiguo Feng, Yue Xu, Chuong D Hoang, Maximilian Diehn, and Ash A Alizadeh. 2015. “Robust enumeration of cell subsets from tissue expression profiles.” Nat. Methods 12 (5). Nature Publishing Group: 453–57. doi:10.1038/nmeth.3337.

Yoshihara, Kosuke, Maria Shahmoradgoli, Emmanuel Martínez, Rahulsimham Vegesna, Hoon Kim, Wandaliz Torres-Garcia, Victor Treviño, et al. 2013. “Inferring tumour purity and stromal and immune cell admixture from expression data.” Nat. Commun. 4 (1). Nature Publishing Group: 2612. doi:10.1038/ncomms3612.

Shen-Orr, Shai S, Robert Tibshirani, Purvesh Khatri, Dale L Bodian, Frank Staedtler, Nicholas M Perry, Trevor Hastie, Minnie M Sarwal, Mark M Davis, and Atul J Butte. 2010. “Cell type–specific gene expression differences in complex tissues.” Nat. Methods 7 (4). Nature Publishing Group: 287–89. doi:10.1038/nmeth.1439.

Moffitt, Richard A, Raoud Marayati, Elizabeth L Flate, Keith E Volmar, S Gabriela Herrera Loeza, Katherine A Hoadley, Naim U Rashid, et al. 2015. “Virtual microdissection identifies distinct tumor- and stroma-specific subtypes of pancreatic ductal adenocarcinoma.” Nat. Genet. 47 (10). Nature Publishing Group: 1168–78. doi:10.1038/ng.3398.

Gaujoux, Renaud, and Cathal Seoighe. 2012. “Semi-supervised Nonnegative Matrix Factorization for gene expression deconvolution: A case study.” Infect. Genet. Evol. 12 (5). Elsevier: 913–21. doi:10.1016/J.MEEGID.2011.08.014.

Thorsson, Vésteinn, David L Gibbs, Scott D Brown, Denise Wolf, Dante S Bortone, Tai-Hsien Ou Yang, Eduard Porta-Pardo, et al. 2018. “The Immune Landscape of Cancer.” Immunity 48 (4). Elsevier: 812–830.e14. doi:10.1016/j.immuni.2018.03.023.

Li, Bo, Jun S. Liu, and X. Shirley Liu. 2017. “Revisit linear regression-based deconvolution methods for tumor gene expression data.” Genome Biol. 18 (1). BioMed Central: 127. doi:10.1186/s13059-017-1256-5.

Tamborero, David, Carlota Rubio-Perez, Ferran Muinos, Radhakrishnan Sabarinathan, Josep Maria Piulats, Aura Muntasell, Rodrigo Dienstmann, Nuria Lopez-Bigas, and Abel Gonzalez-Perez. 2018. “A pan-cancer landscape of interactions between solid tumors and infiltrating immune cell populations.” Clin. Cancer Res. American Association for Cancer Research, clincanres.3509.2017. doi:10.1158/1078-0432.CCR-17-3509.

Racle, Julien, Kaat de Jonge, Petra Baumgaertner, Daniel E Speiser, and David Gfeller. 2017. “Simultaneous enumeration of cancer and immune cell types from bulk tumor gene expression data.” Elife 6. eLife Sciences Publications Limited: e26476. doi:10.7554/eLife.26476.

Finotello, Francesca, Clemens Mayer, Christina Plattner, Gerhard Laschober, Dietmar Rieder, Hubert Hackl, Anne Krogsdam, et al. 2017. “quanTIseq: quantifying immune contexture of human tumors.” bioRxiv. Cold Spring Harbor Laboratory, 223180. doi:10.1101/223180.

Zaslavsky, Maxim E, Jacqueline Buros Novik, Eliza J Chang, and Jeffrey E Hammerbacher. 2017. “Infino: a Bayesian hierarchical model improves estimates of immune infiltration into tumor microenvironment.” bioRxiv. Cold Spring Harbor Laboratory, 221671. doi:10.1101/221671.

Aran, Dvir, Zicheng Hu, and Atul J. Butte. 2017. “xCell: digitally portraying the tissue cellular heterogeneity landscape.” Genome Biol. 18 (1). BioMed Central: 220. doi:10.1186/s13059-017-1349-1.

Onuchic, Vitor, Ryan J. Hartmaier, David N. Boone, Michael L. Samuels, Ronak Y. Patel, Wendy M. White, Vesna D. Garovic, et al. 2016. “Epigenomic Deconvolution of Breast Tumors Reveals Metabolic Coupling between Constituent Cell Types.” Cell Rep. 17 (8): 2075–86. doi:10.1016/j.celrep.2016.10.057.

Li, Yi, and Xiaohui Xie. 2013. “A mixture model for expression deconvolution from RNA-seq in heterogeneous tissues.” BMC Bioinforma. 2013 145 14 (5). BioMed Central: S11. doi:10.1186/1471-2105-14-s5-s11.

Steuerman, Yael, and Irit Gat-Viks. 2016. “Exploiting Gene-Expression Deconvolution to Probe the Genetics of the Immune System.” Edited by Gary A. Churchill. PLOS Comput. Biol. 12 (4). Public Library of Science: e1004856. doi:10.1371/journal.pcbi.1004856.

Gosink, Mark M., Howard T. Petrie, and Nicholas F. Tsinoremas. 2007. “Electronically subtracting expression patterns from a mixed cell population.” Bioinformatics 23 (24). Oxford University Press: 3328–34. doi:10.1093/bioinformatics/btm508.

Drucker, Harris, Christopher J C Burges, Linda Kaufman, Alex J Smola, and Vladimir Vapnik. 1997. “Support vector regression machines.” In Adv. Neural Inf. Process. Syst., 155–61.

Schölkopf, Bernhard, Alex J. Smola, Robert C. Williamson, and Peter L. Bartlett. 2000. “New Support Vector Algorithms.” Neural Comput. 12 (5). MIT Press: 1207–45. doi:10.1162/089976600300015565.

Ju, Wenjun, Casey S Greene, Felix Eichinger, Viji Nair, Jeffrey B Hodgin, Markus Bitzer, Young-Suk Lee, et al. 2013. “Defining cell-type specificity at the transcriptional level in human disease.” Genome Res. 23 (11). Cold Spring Harbor Laboratory Press: 1862–73. doi:10.1101/gr.155697.113.

Repsilber, Dirk, Sabine Kern, Anna Telaar, Gerhard Walzl, Gillian F Black, Joachim Selbig, Shreemanta K Parida, Stefan HE Kaufmann, and Marc Jacobsen. 2010. “Biomarker discovery in heterogeneous tissue samples -taking the in-silico deconfounding approach.” BMC Bioinformatics 11 (1). BioMed Central: 27. doi:10.1186/1471-2105-11-27.

Zuckerman, Neta S., Yair Noam, Andrea J. Goldsmith, and Peter P. Lee. 2013. “A Self-Directed Method for Cell-Type Identification and Separation of Gene Expression Microarrays.” Edited by Teresa M. Przytycka. PLoS Comput. Biol. 9 (8). Public Library of Science: e1003189. doi:10.1371/journal.pcbi.1003189.

Wang, Niya, Eric P. Hoffman, Lulu Chen, Li Chen, Zhen Zhang, Chunyu Liu, Guoqiang Yu, David M. Herrington, Robert Clarke, and Yue Wang. 2016. “Mathematical modelling of transcriptional heterogeneity identifies novel markers and subpopulations in complex tissues.” Sci. Rep. 6 (1). Nature Publishing Group: 18909. doi:10.1038/srep18909.

Lu, Peng, Aleksey Nakorchevskiy, and Edward M Marcotte. 2003. “Expression deconvolution: a reinterpretation of DNA microarray data reveals dynamic changes in cell populations.” Proc. Natl. Acad. Sci. U. S. A. 100 (18). National Academy of Sciences: 10370–5. doi:10.1073/pnas.1832361100.

Wang, Min, Stephen R Master, and Lewis A Chodosh. 2006. “Computational expression deconvolution in a complex mammalian organ.” BMC Bioinformatics 7 (1). BioMed Central: 328. doi:10.1186/1471-2105-7-328.

Gong, Ting, Nicole Hartmann, Isaac S. Kohane, Volker Brinkmann, Frank Staedtler, Martin Letzkus, Sandrine Bongiovanni, and Joseph D. Szustakowski. 2011. “Optimal Deconvolution of Transcriptional Profiling Data Using Quadratic Programming with Application to Complex Clinical Blood Samples.” Edited by Magnus Rattray. PLoS One 6 (11). Public Library of Science: e27156. doi:10.1371/journal.pone.0027156.

Mohammadi, Shahin, Neta Zuckerman, Andrea Goldsmith, and Ananth Grama. 2017. “A Critical Survey of Deconvolution Methods for Separating Cell Types in Complex Tissues.” Proc. IEEE 105 (2): 340–66. doi:10.1109/JPROC.2016.2607121.

Görtler, Franziska, Stefan Solbrig, Tilo Wettig, Peter J. Oefner, Rainer Spang, and Michael Altenbuchinger. 2018. “Loss-function learning for digital tissue deconvolution.” http://arxiv.org/abs/1801.08447.

Chen, Shu-Hwa, Wen-Yu Kuo, Sheng-Yao Su, Wei-Chun Chung, Jen-Ming Ho, Henry Horng-Shing Lu, and Chung-Yen Lin. 2018. “A gene profiling deconvolution approach to estimating immune cell composition from complex tissues.” BMC Bioinformatics 19 (S4). BioMed Central: 154. doi:10.1186/s12859-018-2069-6.

Schelker, Max, Sonia Feau, Jinyan Du, Nav Ranu, Edda Klipp, Birgit Schoeberl, Gavin MacBeath, et al. 2017. “Estimation of immune cell content in tumour tissue using single-cell RNA-seq data.” Nat. Commun. 8 (1). Nature Publishing Group: 2032. doi:10.1038/s41467-017-02289-3.

Liebner, David A., Kun Huang, and Jeffrey D. Parvin. 2014. “MMAD: microarray microdissection with analysis of differences is a computational tool for deconvoluting cell type-specific contributions from tissue samples.” Bioinformatics 30 (5). Oxford University Press: 682–89. doi:10.1093/bioinformatics/btt566.

Newman, AM, CL Liu, and AA Alizadeh. 2018. “CIBERSORT- Absolute mode.” Accessed June 4. https://cibersort.stanford.edu/manual.php.

Subramanian, Aravind, Pablo Tamayo, Vamsi K Mootha, Sayan Mukherjee, Benjamin L Ebert, Michael A Gillette, Amanda Paulovich, et al. 2005. “Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles.” Proc. Natl. Acad. Sci. U. S. A. 102 (43). National Academy of Sciences: 15545–50. doi:10.1073/pnas.0506580102.

Barbie, David A., Pablo Tamayo, Jesse S. Boehm, So Young Kim, Susan E. Moody, Ian F. Dunn, Anna C. Schinzel, et al. 2009. “Systematic RNA interference reveals that oncogenic KRAS-driven cancers require TBK1.” Nature 462 (7269). Nature Publishing Group: 108–12. doi:10.1038/nature08460.

Şenbabaoğlu, Yasin, Ron S. Gejman, Andrew G. Winer, Ming Liu, Eliezer M. Van Allen, Guillermo de Velasco, Diana Miao, et al. 2016. “Tumor immune microenvironment characterization in clear cell renal cell carcinoma identifies prognostic and immunotherapeutically relevant messenger RNA signatures.” Genome Biol. 17 (1). BioMed Central: 231. doi:10.1186/s13059-016-1092-z.

Hänzelmann, Sonja, Robert Castelo, and Justin Guinney. 2013. “GSVA: gene set variation analysis for microarray and RNA-Seq data.” BMC Bioinformatics 14 (1). BioMed Central: 7. doi:10.1186/1471-2105-14-7.

Becht, Etienne, Aurélien de Reyniès, Nicolas A Giraldo, Camilla Pilati, Bénédicte Buttard, Laetitia Lacroix, Janick Selves, Catherine Sautès-Fridman, Pierre Laurent-Puig, and Wolf Herman Fridman. 2016. “Immune and Stromal Classification of Colorectal Cancer Is Associated with Molecular Subtypes and Relevant for Precision Immunotherapy.” Clin. Cancer Res. 22 (16). American Association for Cancer Research: 4057–66. doi:10.1158/1078-0432.CCR-15-2879.

Erkkilä, Timo, Saara Lehmusvaara, Pekka Ruusuvuori, Tapio Visakorpi, Ilya Shmulevich, and Harri Lähdesmäki. 2010. “Probabilistic analysis of gene expression measurements from heterogeneous tissues.” Bioinformatics 26 (20). Oxford University Press: 2571–7. doi:10.1093/bioinformatics/btq406.

Ghosh, D. 2004. “Mixture models for assessing differential expression in complex tissues using microarray data.” Bioinformatics 20 (11). Oxford University Press: 1663–9. doi:10.1093/bioinformatics/bth139.

Lähdesmäki, Harri, llya Shmulevich, Valerie Dunmire, Olli Yli-Harja, and Wei Zhang. 2005. “In silico microdissection of microarray data from heterogeneous cell populations.” BMC Bioinformatics 6 (1). BioMed Central: 54. doi:10.1186/1471-2105-6-54.

Roy, Sushmita, Terran Lane, Chris Allen, Anthony D. Aragon, and Margaret Werner-Washburne. 2006. “A Hidden-State Markov Model for Cell Population Deconvolution.” J. Comput. Biol. 13 (10). Mary Ann Liebert, Inc. 2 Madison Avenue Larchmont, NY 10538 USA: 1749–74. doi:10.1089/cmb.2006.13.1749.

Wang, Zeya, Shaolong Cao, Jeffrey S. Morris, Jaeil Ahn, Rongjie Liu, Svitlana Tyekucheva, Fan Gao, et al. 2017. “Transcriptome Deconvolution of Heterogeneous Tumor Samples with Immune Infiltration.” bioRxiv. Cold Spring Harbor Laboratory, 146795. doi:10.1101/146795.

Yang, Zuyuan, Yong Xiang, Yue Rong, and Kan Xie. 2015. “A Convex Geometry-Based Blind Source Separation Method for Separating Nonnegative Sources.” IEEE Trans. Neural Networks Learn. Syst. 26 (8): 1635–44. doi:10.1109/TNNLS.2014.2350026.

Preparata, Franco P., and Michael Ian Shamos. 1985. “Convex Hulls: Basic Algorithms.” In Comput. Geom., 95–149. New York, NY: Springer New York. doi:10.1007/978-1-4612-1098-6_3.

Erickson, Jeff. 2018. “Jeff Erickson’s Algorithms, Etc.” Accessed June 5. http://jeffe.cs.illinois.edu/teaching/algorithms/.

Shoval, O., H. Sheftel, G. Shinar, Y. Hart, O. Ramote, A. Mayo, E. Dekel, K. Kavanagh, and U. Alon. 2012. “Evolutionary Trade-Offs, Pareto Optimality, and the Geometry of Phenotype Space.” Science (80-. ). 336 (6085): 1157–60. doi:10.1126/science.1217405.

Wang, Niya, Fan Meng, Li Chen, Subha Madhavan, Robert Clarke, Eric P Hoffman, Jianhua Xuan, and Yue Wang. 2013. “The CAM Software for Nonnegative Blind Source Separation in R-Java.” J. Mach. Learn. Res. 14: 2899–2903. http://www.jmlr.org/papers/volume14/wang13d/wang13d.pdf.

Fa-Yu Wang, Chong-Yung Chi, Tsung-Han Chan, and Yue Wang. 2010. “Nonnegative Least-Correlated Component Analysis for Separation of Dependent Sources by Volume Maximization.” IEEE Trans. Pattern Anal. Mach. Intell. 32 (5): 875–88. doi:10.1109/TPAMI.2009.72.

Newberg, Lee A., Xiaowei Chen, Chinnappa D. Kodira, and Maria I. Zavodszky. 2018. “Computational de novo discovery of distinguishing genes for biological processes and cell types in complex tissues.” Edited by Paolo Provero. PLoS One 13 (3). Public Library of Science: e0193067. doi:10.1371/journal.pone.0193067.

Arora, Sanjeev, Rong Ge, Yoni Halpern, David Mimno, Ankur Moitra, David Sontag, Yichen Wu, and Michael Zhu. 2013. “A practical algorithm for topic modeling with provable guarantees.” JMLR.org. https://dl.acm.org/citation.cfm?id=3042925.

Zinovyev, Andrei, Ulykbek Kairov, Tatyana Karpenyuk, and Erlan Ramanculov. 2013. “Blind source separation methods for deconvolution of complex signals in cancer biology.” Biochem. Biophys. Res. Commun. 430 (3). Academic Press: 1182–7. doi:10.1016/J.BBRC.2012.12.043.

Rutledge, D.N., and D. Jouan-Rimbaud Bouveresse. 2013. “Independent Components Analysis with the JADE algorithm.” TrAC Trends Anal. Chem. 50. Elsevier: 22–32. doi:10.1016/J.TRAC.2013.03.013.

Wang, Niya, Ting Gong, Robert Clarke, Lulu Chen, Ie-Ming Shih, Zhen Zhang, Douglas A. Levine, Jianhua Xuan, and Yue Wang. 2015. “UNDO: a Bioconductor R package for unsupervised deconvolution of mixed gene expressions in tumor samples.” Bioinformatics 31 (1). Oxford University Press: 137–39. doi:10.1093/bioinformatics/btu607.

Nelms, Bradlee D., Levi Waldron, Luis A. Barrera, Andrew W. Weflen, Jeremy A. Goettel, Guoji Guo, Robert K. Montgomery, et al. 2016. “CellMapper: rapid and accurate inference of gene expression in difficult-to-isolate cell types.” Genome Biol. 17 (1). BioMed Central: 201. doi:10.1186/s13059-016-1062-5.

Seung, H. Sebastian, and Daniel D. Lee. 1999. “Learning the parts of objects by non-negative matrix factorization.” Nature 401 (6755). Nature Publishing Group: 788–91. doi:10.1038/44565.

Paatero, Pentti, and Unto Tapper. 1994. “Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values.” Environmetrics 5 (2). Wiley-Blackwell: 111–26. doi:10.1002/env.3170050203.

Lin, Chih-Jen. 2007. “Projected Gradient Methods for Nonnegative Matrix Factorization.” Neural Comput. 19 (10). MIT Press 238 Main St., Suite 500, Cambridge, MA 02142-1046 USA journals-info@mit.edu: 2756–79. doi:10.1162/neco.2007.19.10.2756.

Ding, C.H.Q., Tao Li, and M.I. Jordan. 2010. “Convex and Semi-Nonnegative Matrix Factorizations.” IEEE Trans. Pattern Anal. Mach. Intell. 32 (1): 45–55. doi:10.1109/TPAMI.2008.277.

Ortega-Martorell, Sandra, Paulo J.G. Lisboa, Alfredo Vellido, Margarida Julia-Sape, and Carles Arus. 2012. “Non-negative Matrix Factorisation methods for the spectral decomposition of MRS data from human brain tumours.” BMC Bioinformatics 13 (1). BioMed Central: 38. doi:10.1186/1471-2105-13-38.

Brunet, Jean-Philippe, Pablo Tamayo, Todd R Golub, and Jill P Mesirov. 2004. “Metagenes and molecular pattern discovery using matrix factorization.” Proc. Natl. Acad. Sci. U. S. A. 101 (12). National Academy of Sciences: 4164–9. doi:10.1073/pnas.0308531101.

Lee, Daniel D., and H. Sebastian Seung. 2000. “Algorithms for non-negative matrix factorization.” MIT Press. https://dl.acm.org/citation.cfm?id=3008829.

Gaujoux, R., and C. Seoighe. 2013. “CellMix: a comprehensive toolbox for gene expression deconvolution.” Bioinformatics 29 (17): 2211–2. doi:10.1093/bioinformatics/btt351.

Gaujoux, Renaud, and Cathal Seoighe. 2010. “A flexible R package for nonnegative matrix factorization.” BMC Bioinformatics 11 (1). BioMed Central: 367. doi:10.1186/1471-2105-11-367.

Pascual-Montano, A., J.M. Carazo, K. Kochi, D. Lehmann, and R.D. Pascual-Marqui. 2006. “Nonsmooth nonnegative matrix factorization (nsNMF).” IEEE Trans. Pattern Anal. Mach. Intell. 28 (3): 403–15. doi:10.1109/TPAMI.2006.60.

Liu, Yuan, Yu Liang, Qifan Kuang, Fanfan Xie, Yingyi Hao, Zhining Wen, and Menglong Li. 2017. “Post-modified non-negative matrix factorization for deconvoluting the gene expression profiles of specific cell types from heterogeneous clinical samples based on RNA-sequencing data.” J. Chemom. Wiley-Blackwell, e2929. doi:10.1002/cem.2929.

Herault, J., and C. Jutten. 1986. “Space or time adaptive signal processing by neural network models.” In AIP Conf. Proc., 151:206–11. 1. AIP. doi:10.1063/1.36258.

Hyvärinen, Aapo, and Erkki Oja. 2000. “Independent Component Analysis: Algorithms and Applications.” Neural Networks 13 (45): 411–30. https://www.cs.helsinki.fi/u/ahyvarin/papers/NN00new.pdf.

Bell, Anthony J, and Terrence J Sejnowski. 1995. “An information-maximisation approach to blind separation and blind deconvolution.” http://www.inf.fu-berlin.de/lehre/WS05/Mustererkennung/infomax/infomax.pdf.

Cardoso, J.F., and A. Souloumiac. 1993. “Blind beamforming for non-gaussian signals.” IEE Proc. F Radar Signal Process. 140 (6): 362. doi:10.1049/ip-f-2.1993.0054.

Teschendorff, Andrew E., Michel Journée, Pierre A. Absil, Rodolphe Sepulchre, and Carlos Caldas. 2007. “Elucidating the Altered Transcriptional Programs in Breast Cancer using Independent Component Analysis.” PLoS Comput. Biol. 3 (8). Public Library of Science: e161. doi:10.1371/journal.pcbi.0030161.

Biton, Anne, Isabelle Bernard-Pierrot, Yinjun Lou, Clémentine Krucker, Elodie Chapeaublanc, Carlota Rubio-Pérez, Nuria López-Bigas, et al. 2014. “Independent Component Analysis Uncovers the Landscape of the Bladder Tumor Transcriptome and Reveals Insights into Luminal and Basal Subtypes.” Cell Rep. 9 (4): 1235–45. doi:10.1016/j.celrep.2014.10.035.

Engreitz, Jesse M, Bernie J Daigle, Jonathan J Marshall, Russ B Altman, and Russ B. Altman. 2010. “Independent component analysis: mining microarray data for fundamental human gene expression modules.” J. Biomed. Inform. 43 (6). NIH Public Access: 932–44. doi:10.1016/j.jbi.2010.07.001.

Gorban, A. N. (Aleksandr Nikolaevich). 2007. Principal manifolds for data visualization and dimension reduction. Springer.

Cantini, Laura, Ulykbek Kairov, Aurelien de Reynies, Emmanuel Barillot, Francois Radvanyi, and Andrei Zinovyev. 2018. “Stabilized Independent Component Analysis outperforms other methods in finding reproducible signals in tumoral transcriptomes.” bioRxiv. Cold Spring Harbor Laboratory, 318154. doi:10.1101/318154.

Cheng, Wei-Yi, Tai-Hsien Ou Yang, and Dimitris Anastassiou. 2013. “Biomolecular Events in Cancer Revealed by Attractor Metagenes.” Edited by Isidore Rigoutsos. PLoS Comput. Biol. 9 (2). Public Library of Science: e1002920. doi:10.1371/journal.pcbi.1002920.

Al-Ejeh, F, P T Simpson, J M Sanus, K Klein, M Kalimutho, W Shi, M Miranda, et al. 2014. “Meta-analysis of the global gene expression profile of triple-negative breast cancer identifies genes for the prognostication and treatment of aggressive breast cancer.” Oncogenesis 3 (4). Nature Publishing Group: e100–e100. doi:10.1038/oncsis.2014.14.

Elmas, Abdulkadir, Tai-Hsien Ou Yang, Xiaodong Wang, and Dimitris Anastassiou. 2016. “Discovering Genome-Wide Tag SNPs Based on the Mutual Information of the Variants.” Edited by Srinivas Mummidi. PLoS One 11 (12). Public Library of Science: e0167994. doi:10.1371/journal.pone.0167994.

Vallania, Francesco, Andrew Tam, Shane Lofgren, Steven Schaffert, Tej D. Azad, Erika Bongen, Meia Alsup, et al. 2017. “Leveraging heterogeneity across multiple data sets increases accuracy of cell-mixture deconvolution and reduces biological and technical biases.” bioRxiv. Cold Spring Harbor Laboratory, 206466. doi:10.1101/206466.

Hoffmann, Martin, Dirk Pohlers, Dirk Koczan, Hans-Jürgen Thiesen, Stefan Wölfl, and Raimund W Kinne. 2006. “Robust computational reconstitution – a new method for the comparative analysis of gene expression in tissues and isolated cell fractions.” BMC Bioinformatics 7 (1). BioMed Central: 369. doi:10.1186/1471-2105-7-369.

Qiao, Wenlian, Gerald Quon, Elizabeth Csaszar, Mei Yu, Quaid Morris, and Peter W. Zandstra. 2012. “PERT: A Method for Expression Deconvolution of Human Blood Samples from Varied Microenvironmental and Developmental Conditions.” Edited by Richard Bonneau. PLoS Comput. Biol. 8 (12). Public Library of Science: e1002838. doi:10.1371/journal.pcbi.1002838.

Chung, Woosung, Hye Hyeon Eum, Hae-Ock Lee, Kyung-Min Lee, Han-Byoel Lee, Kyu-Tae Kim, Han Suk Ryu, et al. 2017. “Single-cell RNA-seq enables comprehensive tumour and immune cell profiling in primary breast cancer.” Nat. Commun. 8. Nature Publishing Group: 15081. doi:10.1038/ncomms15081.

Lavin, Yonit, Soma Kobayashi, Andrew Leader, El-ad David Amir, Naama Elefant, Camille Bigenwald, Romain Remark, et al. 2017. “Innate Immune Landscape in Early Lung Adenocarcinoma by Paired Single-Cell Analyses.” Cell 169 (4). Cell Press: 750–765.e17. doi:10.1016/J.CELL.2017.04.014.

Puram, Sidharth V., Itay Tirosh, Anuraag S. Parikh, Anoop P. Patel, Keren Yizhak, Shawn Gillespie, Christopher Rodman, et al. 2017. “Single-Cell Transcriptomic Analysis of Primary and Metastatic Tumor Ecosystems in Head and Neck Cancer.” Cell 171 (7). Cell Press: 1611–1624.e24. doi:10.1016/J.CELL.2017.10.044.

Tirosh, Itay, Benjamin Izar, Sanjay M. Prakadan, Marc H. Wadsworth, Daniel Treacy, John J. Trombetta, Asaf Rotem, et al. 2016. “Dissecting the multicellular ecosystem of metastatic melanoma by single-cell RNA-seq.” Science (80-. ). 352 (6282): 189–96. doi:10.1126/science.aad0501.

Zheng, Chunhong, Liangtao Zheng, Jae-Kwang Yoo, Huahu Guo, Yuanyuan Zhang, Xinyi Guo, Boxi Kang, et al. 2017. “Landscape of Infiltrating T Cells in Liver Cancer Revealed by Single-Cell Sequencing.” Cell 169 (7). Cell Press: 1342–1356.e16. doi:10.1016/J.CELL.2017.05.035.

Hoyle, David C, Magnus Rattray, Ray Jupp, and Andrew Brass. 2002. “Making sense of microarray data distributions.” Bioinformatics 18 (4): 576–84. http://www.ncbi.nlm.nih.gov/pubmed/12016055.

Tsai, Chen-An, Yi-Ju Chen, and James J Chen. 2003. “Testing for differentially expressed genes with microarray data.” Nucleic Acids Res. 31 (9): e52. http://www.ncbi.nlm.nih.gov/pubmed/12711697 http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC154240.

Zhong, Yi, Ying-Wooi Wan, Kaifang Pang, Lionel ML Chow, and Zhandong Liu. 2013. “Digital sorting of complex tissues for cell type-specific gene expression profiles.” BMC Bioinformatics 14 (1). BioMed Central: 89. doi:10.1186/1471-2105-14-89.

Shannon, Casey P., Robert Balshaw, Virginia Chen, Zsuzsanna Hollander, Mustafa Toma, Bruce M. McManus, J. Mark FitzGerald, Don D. Sin, Raymond T. Ng, and Scott J. Tebbutt. 2017. “Enumerateblood – an R package to estimate the cellular composition of whole blood from Affymetrix Gene ST gene expression profiles.” BMC Genomics 18 (1). BioMed Central: 43. doi:10.1186/s12864-016-3460-1.

Clarke, J., P. Seo, and B. Clarke. 2010. “Statistical expression deconvolution from mixed tissue samples.” Bioinformatics 26 (8). Oxford University Press: 1043–9. doi:10.1093/bioinformatics/btq097.

Jin, Haijing, Ying-Wooi Wan, and Zhandong Liu. 2017. “Comprehensive evaluation of RNA-seq quantification methods for linearity.” BMC Bioinformatics 18 (S4). BioMed Central: 117. doi:10.1186/s12859-017-1526-y.

Kuhn, Alexandre, Doris Thu, Henry J Waldvogel, Richard L M Faull, and Ruth Luthi-Carter. 2011. “Population-specific expression analysis (PSEA) reveals molecular changes in diseased brain.” Nat. Methods 8 (11). Nature Publishing Group: 945–47. doi:10.1038/nmeth.1710.

Li, Bo, Eric Severson, Jean-Christophe Pignon, Haoquan Zhao, Taiwen Li, Jesse Novak, Peng Jiang, et al. 2016. “Comprehensive analyses of tumor immunity: implications for cancer immunotherapy.” Genome Biol. 17 (1). BioMed Central: 174. doi:10.1186/s13059-016-1028-7.

Cieślik, Marcin, and Arul M. Chinnaiyan. 2017. “Cancer transcriptome profiling at the juncture of clinical translation.” Nat. Rev. Genet. 19 (2). Nature Publishing Group: 93–109. doi:10.1038/nrg.2017.96.

Regev, Aviv, Sarah A Teichmann, Eric S Lander, Ido Amit, Christophe Benoist, Ewan Birney, Bernd Bodenmiller, et al. 2017. “The Human Cell Atlas.” Elife 6. eLife Sciences Publications Limited: e27041. doi:10.7554/eLife.27041.

Teschendorff, Andrew E, and Shijie C Zheng. 2017. “Cell-type deconvolution in epigenome-wide association studies: a review and recommendations.” Epigenomics 9 (5): 757–68. doi:10.2217/epi-2016-0153.

Titus, Alexander J., Rachel M. Gallimore, Lucas A. Salas, and Brock C. Christensen. 2017. “Cell-type deconvolution from DNA methylation: a review of recent applications.” Hum. Mol. Genet. 26 (R2): R216–R224. doi:10.1093/hmg/ddx275.

Houseman, Eugene Andres, John Molitor, and Carmen J. Marsit. 2014. “Reference-free cell mixture adjustments in analysis of DNA methylation data.” Bioinformatics 30 (10). Oxford University Press: 1431–9. doi:10.1093/bioinformatics/btu029.

Leek, Jeffrey T., and John D. Storey. 2007. “Capturing Heterogeneity in Gene Expression Studies by Surrogate Variable Analysis.” PLoS Genet. 3 (9): e161. doi:10.1371/journal.pgen.0030161.

Teschendorff, Andrew E., Joanna Zhuang, and Martin Widschwendter. 2011. “Independent surrogate variable analysis to deconvolve confounding factors in large-scale microarray profiling studies.” Bioinformatics 27 (11). Oxford University Press: 1496–1505. doi:10.1093/bioinformatics/btr171.

Maksimovic, Jovana, Johann A. Gagnon-Bartsch, Terence P. Speed, and Alicia Oshlack. 2015. “Removing unwanted variation in a differential methylation analysis of Illumina HumanMethylation450 array data.” Nucleic Acids Res. 43 (16). Oxford University Press: e106–e106. doi:10.1093/nar/gkv526.

Zou, James, Christoph Lippert, David Heckerman, Martin Aryee, and Jennifer Listgarten. 2014. “Epigenome-wide association studies without the need for cell-type composition.” Nat. Methods 11 (3). Nature Publishing Group: 309–11. doi:10.1038/nmeth.2815.

Rahmani, Elior, Noah Zaitlen, Yael Baran, Celeste Eng, Donglei Hu, Joshua Galanter, Sam Oh, et al. 2016. “Sparse PCA corrects for cell type heterogeneity in epigenome-wide association studies.” Nat. Methods 13 (5). Nature Publishing Group: 443–45. doi:10.1038/nmeth.3809.

Houseman, E. Andres, Molly L. Kile, David C. Christiani, Tan A. Ince, Karl T. Kelsey, and Carmen J. Marsit. 2016. “Reference-free deconvolution of DNA methylation data and mediation by cell composition effects.” BMC Bioinformatics 17 (1). BioMed Central: 259. doi:10.1186/s12859-016-1140-4.

Lutsik, Pavlo, Martin Slawski, Gilles Gasparoni, Nikita Vedeneev, Matthias Hein, and Jörn Walter. 2017. “MeDeCom: discovery and quantification of latent components of heterogeneous methylomes.” Genome Biol. 18 (1). BioMed Central: 55. doi:10.1186/s13059-017-1182-6.

Houseman, Eugene, William P Accomando, Devin C Koestler, Brock C Christensen, Carmen J Marsit, Heather H Nelson, John K Wiencke, and Karl T Kelsey. 2012. “DNA methylation arrays as surrogate measures of cell mixture distribution.” BMC Bioinformatics 13 (1). BioMed Central: 86. doi:10.1186/1471-2105-13-86.

Breeze, Charles E., Dirk S. Paul, Jenny van Dongen, Lee M. Butcher, John C. Ambrose, James E. Barrett, Robert Lowe, et al. 2016. “eFORGE: A Tool for Identifying Cell Type-Specific Signal in Epigenomic Data.” Cell Rep. 17 (8): 2137–50. doi:10.1016/j.celrep.2016.10.059.

Wen, Yanhua, Yanjun Wei, Shumei Zhang, Song Li, Hongbo Liu, Fang Wang, Yue Zhao, Dongwei Zhang, and Yan Zhang. 2016. “Cell subpopulation deconvolution reveals breast cancer heterogeneity based on DNA methylation signature.” Brief. Bioinform. 18 (3): bbw028. doi:10.1093/bib/bbw028.

Aran, Dvir, Marina Sirota, and Atul J Butte. 2015. “Systematic pan-cancer analysis of tumour purity.” Nat. Commun. 6. Nature Publishing Group: 8971. doi:10.1038/ncomms9971.

Fu, Yi, Guoqiang Yu, Douglas A. Levine, Niya Wang, Ie-Ming Shih, Zhen Zhang, Robert Clarke, and Yue Wang. 2015. “BACOM2.0 facilitates absolute normalization and quantification of somatic copy number alterations in heterogeneous tumor.” Sci. Rep. 5 (1). Nature Publishing Group: 13955. doi:10.1038/srep13955.

Carter, Scott L, Kristian Cibulskis, Elena Helman, Aaron McKenna, Hui Shen, Travis Zack, Peter W Laird, et al. 2012. “Absolute quantification of somatic DNA alterations in human cancer.” Nat. Biotechnol. 30 (5). Nature Publishing Group: 413–21. doi:10.1038/nbt.2203.

Yu, Zhenhua, Ao Li, and Minghui Wang. 2016. “CloneCNA: detecting subclonal somatic copy number alterations in heterogeneous tumor samples from whole-exome sequencing data.” BMC Bioinformatics 17 (1): 310. doi:10.1186/s12859-016-1174-7.

Larson, Nicholas B, and Brooke L Fridley. 2013. “PurBayes: estimating tumor cellularity and subclonality in next-generation sequencing data.” Bioinformatics 29 (15). Oxford University Press: 1888–9. doi:10.1093/bioinformatics/btt293.

Li, Bo, and Jun Z Li. 2014. “A general framework for analyzing tumor subclonality using SNP array and DNA sequencing data.” Genome Biol. 15 (9). BioMed Central: 473. doi:10.1186/s13059-014-0473-4.

Oesper, Layla, Ahmad Mahmoody, and Benjamin J Raphael. 2013. “THetA: inferring intra-tumor heterogeneity from high-throughput DNA sequencing data.” Genome Biol. 14 (7). BioMed Central: R80. doi:10.1186/gb-2013-14-7-r80.

Miller, Christopher A., Brian S. White, Nathan D. Dees, Malachi Griffith, John S. Welch, Obi L. Griffith, Ravi Vij, et al. 2014. “SciClone: Inferring Clonal Architecture and Tracking the Spatial and Temporal Patterns of Tumor Evolution.” Edited by Niko Beerenwinkel. PLoS Comput. Biol. 10 (8). Public Library of Science: e1003665. doi:10.1371/journal.pcbi.1003665.

Jiang, Yuchao, Yu Qiu, Andy J Minn, and Nancy R Zhang. 2016. “Assessing intratumor heterogeneity and tracking longitudinal and spatial clonal evolutionary history by next-generation sequencing.” Proc. Natl. Acad. Sci. U. S. A. 113 (37). National Academy of Sciences: E5528–37. doi:10.1073/pnas.1522203113.

Roth, Andrew, Jaswinder Khattra, Damian Yap, Adrian Wan, Emma Laks, Justina Biele, Gavin Ha, Samuel Aparicio, Alexandre Bouchard-Côté, and Sohrab P Shah. 2014. “PyClone: statistical inference of clonal population structure in cancer.” Nat. Methods 11 (4). Nature Publishing Group: 396–98. doi:10.1038/nmeth.2883.

Andor, Noemi, Julie V. Harness, Sabine Müller, Hans W. Mewes, and Claudia Petritsch. 2014. “EXPANDS: expanding ploidy and allele frequency on nested subpopulations.” Bioinformatics 30 (1). Oxford University Press: 50–60. doi:10.1093/bioinformatics/btt622.